Нормальный закон распределения.

Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это — наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других, состоит в том, что он является предельным, к которому приближаются другие законы распределения при весьма часто встречающихся условиях.

Можно доказать, что сумма достаточно большого числа незави­симых случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых — элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному.

Нормальный закон распределения характеризуется плотностью вероятности вида:

(4.6.1)

Кривая распределения по нормальному закону имеет симметрич­ный холмообразный вид (рис. 4.6.1). Максимальная ордината кривой, равная , соответствует точке X=т; по мере удаления от точки т плотность распределения уменьшается, и при кривая асимптотически приближается к оси абсцисс.

Выясним смысл параметров m и 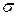, входящих в выражение нормального закона; докажем, что величина т есть не что иное, как математическое ожидание, а величина 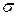— среднеквадратическое отклонение величины X. Для этого вычислим основные числовые характеристики случайной величины Х.

Применяя замену переменной, имеем:

Нетрудно убедиться, что первый из двух интервалов равен нулю; второй представляет собой известный интеграл Эйлера — Пуассона:

(4.6.2)

Следовательно,

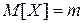
(4.6.3)

Вычислим дисперсию величины X.

(4.6.4)

Применив снова замену переменной, имеем:

Интегрируя по частям, получим:

Первое слагаемое в фигурных скобках равно нулю (так как при 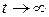убывает быстрее, чем возрастает любая степень t), второе слагаемое равно , откуда .

Следовательно, параметр 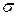есть не что иное, как среднеквадратическое отклонение величины X.

Из соотношения (4.6.1) следует, что центром симметрии распределения является центр рассеивания т. Это ясно из того, что при изменении знака разности (x - т) на обратный выражение (4.6.1) не меняется. Если изменять центр рассеивания т кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 4.6.2).

Параметр 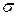характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна 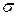; при увеличении 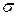максимальная ордината уменьшается.

На рис. 4.6.3 показаны три нормальные кривые (I, II, III) при m = 0; из них кривая I соответствует

самому большому, а кривая III — самому малому значению .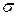

Размерность параметра 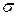, естественно, совпадает с размерностью случайной величины X.