Равномерное распределение.

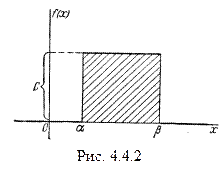
Рассмотрим непрерывную случайную величину X, подчиненную закону равномерной плотности на участке от 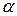до 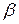(рис. 4.4.2), и напишем для нее выражение плотности распределения f(х). Плотность f(х) постоянна и равна с на отрезке ( 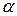; 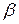); вне этого отрезка она равна нулю:

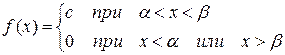
(4.4.1)

Определим постоянную с из условия 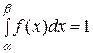, получим

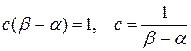
Тогда

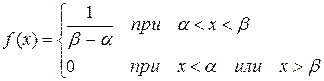
(4.4.2)

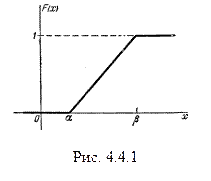
Выражение для функции распределения F(х) равномерно распределенной случайной величины имеет вид:

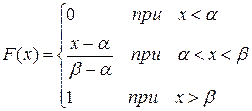
(4.4.3)

График функции F(х) приведен на рис. 4.4.1. Определим основные числовые характеристики случайной величины X, подчиненной закону равномерной плотности на участке от 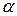до .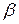

Математическое ожидание величины Х равно:

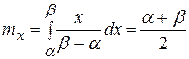
(4.4.4)

В силу симметричности равномерного распределения медиана величины Х также равна .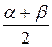

Моды закон равномерной плотности не имеет. Находим дисперсию величиныX:

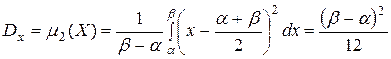
(4.4.5)

откуда среднеквадратическое отклонение 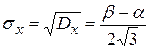. В силу симметричности распределения его асимметрия равна нулю:

(4.4.6)

Найдем вероятность попадания случайной величины X, распределенной по закону равномерной плотности, на участок (a,b), представляющий собой часть участка ( 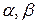)(рис. 4.4.3).

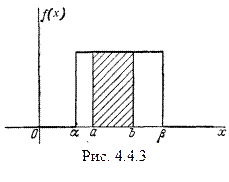
Геометрически эта вероятность представляет собой площадь, заштрихованную на рис. 4.4.3. Очевидно, она равна:

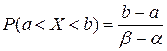
т. е. отношению длины отрезка 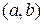ко всей длине участка 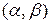, на котором задано равномерное распределение.