Свойства функции распределения.

Свойство 1. Функция распределения любой случайной величины, есть неубывающая функция.

Зная функцию распределения случайной величины X, можно определить вероятность неравенства x₁ 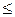X<x₂ при любых 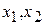. В самом деле, если через A обозначить событие, состоящее в том, что X, примет значение, меньшее чем x₂, через В—событие, состоя­щее в том, что X < x₁, наконец, через С — событие x₁ 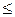X<x₂ ,то, очевидно, имеет место следующее равенство:

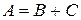
(3.2.1)

Так как события В и С несовместимы, то Р(А)=P(B)+Р(C).

Но

(3.2.2)

поэтому

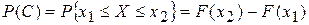
(3.2.3)

Так как, по определению, вероятность есть неотрицательное число, то из равенства (3.2.3) следует, что при любых x₁ и (x₂>x₁) имеет место неравенство

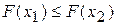
(3.2.4)

что и требовалось доказать.

Свойство 2. . Так как, функция распределения 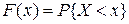, то согласно свойств вероятности 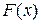при любом х удовлетворяет неравенству

(3.2.5)

Свойство 3. Функция распределения может иметь не более чем счетное множество скачков.

Мы скажем, что функция распределения F(х) имеет при х=x₀ скачок, если

(3.2.6)

В самом деле, скачков размера , функция распределения может иметь не более одного, скачков размера от одной четвертой до половины 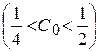- не более трех. Вообще скачков размера от 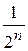до 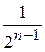может быть не более чем . Совершенно ясно, что мы можем пронумеровать все скачки, расположив их по величине, начиная с больших значений и повторяя равные значения столько раз, сколько скачков этой величины имеет функция F(х).

Свойство 4. 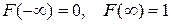. Определи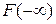м и равенствами

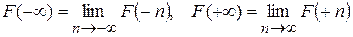
и докажем, что .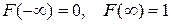

Действительно, так как неравенство X< + достоверно, то

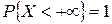
Обозначим через 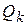событие, состоящее в том, что 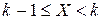. Так как событие 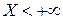, эквивалентно сумме событий 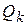, то на основании расширенной аксиомы сложения . Следовательно, при

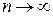
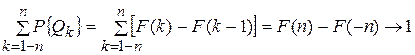
Отсюда, принимая во внимание неравенства (3.2.5), заключаем, что при .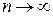

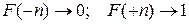Свойство 5. Функция распределения непрерывна слева.

Выберем какую-нибудь возрастающую последовательность 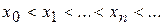, сходящуюся к x.

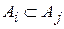Обозначим через A_n, событие . Тогда ясно, что , при i>j, и произведение всех событий A_n, есть невозможное событие. По аксиоме непрерывности должно быть

что и требовалось доказать.