Обобщенная теорема о повторении опытов.

Поставим теперь более общую задачу.

Рассмотрим последовательность n независимых испытаний в каждом из которых может произойти или не произойти некоторое событие А. При этом вероятность появления события в каждом испытании различна.

Обозначим через . А_i – событие состоящее том что А произойдет в i-ом испытании 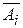– событие состоящее том что А не произойдет в i-ом испытании соответственно.

Следует определить вероятность того что событие А произойдет m раз в серии из n испытаний.

Обозначим через В_m – событие состоящее в том что, событие А произойдет m раз в серии из n испытаний.

(2.2.1)

Здесь А_i – событие состоящее в том, что событие А произойдет в i- ом испытании. Событие В_m представляет собой сумму несовместных событий, поэтому

Число слагаемых в выражении равно , но они все различные. Для вычисления используют производящую функцию

ProizFunc

(2.2.2)

Зададимся целью найти в этом произведении коэффициент при . Для этого перемножим биномы и произведем приведение подобных членов. Каждый член содержащий будет иметь в качестве коэффициента произведение m букв p с какими-то индексами и n-m букв q с другими оставшимися индексами, а после приведения подобных членов коэффициент при будет представлять собой сумму всех возможных произведений такого типа.

Таким образом, вероятность того, что событие А произойдет m раз в серии из n испытаний равна коэффициенту при в выражении производящей функции, то есть

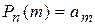
	(2.2.3)
	(2.2.4)

Пример 1. Производится стрельба по бегущей мишени. Вероятность попадания при первом выстреле p₁ =0,1; при втором p₂ =0,2; при третьем p₃ =0,3 и при четвертом p₄ =0,4. Определить вероятность одного, двух, трех, четырех и ни одного попадания при четырех выстрелах.

Решение:

Составляем производящую функцию для данной задачи

Выполняя, элементарные преобразования и приведение подобных членов получаем

Откуда следует, что

- вероятность ни одного попадания в мишень.

- вероятность одного попадания в мишень.

- вероятность двух попаданий в мишень.

- вероятность трех попаданий в мишень.

- вероятность четырех попаданий в мишень.

При решении многих практических задач, кроме определения вероятности , приходится вычислять вероятность появлений события А не менее m раз в n независимых испытаниях.

Обозначим через событие состоящее в том, что А появляется не менее m раз в n независимых испытаниях, а вероятность обозначим , тогда

(2.2.5)

Согласно теоремы сложения вероятностей событий имеем

(2.2.6)

В тех случаях когда удобно пользоваться следующей формулой

(2.2.7)