
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Независимые испытания. Формулы Бернулли.
В настоящем разделе мы изучим основные закономерности, относящиеся к одной из важнейших схем теории вероятностей — схеме последовательных независимых испытаний. В это понятие мы вкладываем следующий смысл.
Под испытанием(опытом) мы станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства U элементарных событий. Математической моделью последовательности п испытаний является новое пространство  элементарных событий, состоящее из точек
элементарных событий, состоящее из точек  , где
, где  - произвольная точка пространства U, отвечающая испытанию с номером i.
- произвольная точка пространства U, отвечающая испытанию с номером i.
Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных состояний состоит из 6 точек. Пространство 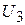 ,соответствующее трем испытаниям, состоит из 216 точек(n=63).
,соответствующее трем испытаниям, состоит из 216 точек(n=63).
Пусть под испытанием понимается проверка длительности безотказной работы полупроводникового прибора под определенным напряжением. Пространство элементарных событий состоит из множества точек полупрямой  . Пространство
. Пространство  состоит из множества точек
состоит из множества точек  , координаты которых принимают неотрицательные значения, равные длительностям безотказной работы соответственно приборов с номерами 1,2,...,n.
, координаты которых принимают неотрицательные значения, равные длительностям безотказной работы соответственно приборов с номерами 1,2,...,n.
Предположим, что для s-го испытания пространство U разбито на k несовместимых случайных событий  , т. е. предположим, что
, т. е. предположим, что

|
Событие  назовем i-м исходом при s-м испытании. Обозначим вероятность i-го исхода при s-м испытании через
назовем i-м исходом при s-м испытании. Обозначим вероятность i-го исхода при s-м испытании через  = Р (
= Р (  ).
).
Bernylli Обозначим через  событие, состоящее из всех тех точек
событие, состоящее из всех тех точек  пространства
пространства  , для которых
, для которых 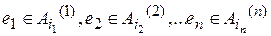 . Если в пространстве Un имеет место равенство
. Если в пространстве Un имеет место равенство  при любых
при любых 
 - то испытания называются независимыми.
- то испытания называются независимыми.
В дальнейшем мы ограничимся случаем, когда вероятности событий  не зависят от номера испытания s; обозначим в этом случае
не зависят от номера испытания s; обозначим в этом случае  ; в силу несовместимости и единственной возможности исходов
; в силу несовместимости и единственной возможности исходов  очевидно, имеем
очевидно, имеем 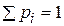 . Эта схема впервые была рассмотрена Я. Бернулли в важнейшем частном случае
. Эта схема впервые была рассмотрена Я. Бернулли в важнейшем частном случае  ; по этой причине указанный случай носит название схемы Бернулли. В схеме Бернулли обычно полагают
; по этой причине указанный случай носит название схемы Бернулли. В схеме Бернулли обычно полагают 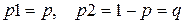 .
.
Из определения независимых испытаний вытекает следующий результат:
Теорема 1. Если данные п испытаний независимы, то любые т из них также независимы.
Для простоты ограничимся случаем  , поскольку переход к общему случаю не встречает затруднений. Действительно, имеет место очевидное равенство
, поскольку переход к общему случаю не встречает затруднений. Действительно, имеет место очевидное равенство

|
из которого следует, что

|
По определению это означает, что первые п—1 испытаний независимы. Простейшая задача, относящаяся к схеме независимых испытаний, состоит в определении вероятности  того, что при п испытаниях событие А наступит т раз, а остальные п—т раз наступит противоположное событие
того, что при п испытаниях событие А наступит т раз, а остальные п—т раз наступит противоположное событие 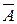 , обозначим это событие В. Тогда
, обозначим это событие В. Тогда

| (2.1.1) |
Здесь Аi – событие состоящее в том, что событие А произойдет в i- ом испытании. Событие В представляет собой сумму несовместных событий, тогда согласно теореме сложения вероятностей получаем

| (2.1.2) |
Вероятность каждого слагаемого в данной сумме по теореме умножения для независимых событий равна  . По теореме сложения вероятностей искомая вероятность
. По теореме сложения вероятностей искомая вероятность  равна сумме только что вычисленных вероятностей для всех различных способов т появлений события А и n—т не появлений среди п испытаний. Число таких способов, как известно из теории сочетаний, равно
равна сумме только что вычисленных вероятностей для всех различных способов т появлений события А и n—т не появлений среди п испытаний. Число таких способов, как известно из теории сочетаний, равно  ; следовательно, искомая вероятность равна
; следовательно, искомая вероятность равна

| (2.1.3) |
Так как все возможные несовместимые между собой исходы п испытаний состоят в появлении события 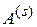 0 раз, 1 раз, 2 раза, ..., n раз, то ясно, что
0 раз, 1 раз, 2 раза, ..., n раз, то ясно, что

| (2.1.4) |
Легко заметить, что вероятность  равна коэффициенту при
равна коэффициенту при  в разложении бинома
в разложении бинома  по степеням x.
по степеням x.
Исследуем далее как ведет себя вероятность при различных значениях m. Найдем m, при котором вероятность  является наибольшей. Для этого определим отношение
является наибольшей. Для этого определим отношение

|
Из полученного соотношения следует:
1) Пусть  - в данном случае вероятность возрастет с ростом m.
- в данном случае вероятность возрастет с ростом m.
2) Пусть  - тогда предыдущая и последующая вероятности выравниваются.
- тогда предыдущая и последующая вероятности выравниваются.
3) Пусть  - в данном случае вероятность уменьшается с ростом m.
- в данном случае вероятность уменьшается с ростом m.
Таким образом,  с увеличением m сначала возрастает, затем достигает максимума и при дальнейшем росте m убывает. При этом, если
с увеличением m сначала возрастает, затем достигает максимума и при дальнейшем росте m убывает. При этом, если  является целым числом, то максимальное значение вероятность
является целым числом, то максимальное значение вероятность  принимает для двух значений m, а именно
принимает для двух значений m, а именно  и
и  . Если же
. Если же  не является целым числом, то максимальное значение вероятности
не является целым числом, то максимальное значение вероятности  достигается при
достигается при  , равном максимальному целому числу, большему из
, равном максимальному целому числу, большему из 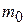 и
и  . Число
. Число  называют наивероятнейшим значением и обозначают через
называют наивероятнейшим значением и обозначают через  .
.
Пример. Вероятность попадания при одном броске в кольцо равна 0,4. Баскетболист совершил 10 бросков. Каково наивероятнейшее значение числа попаданий в кольцо?
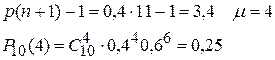
|
Дата добавления: 2014-12-23; просмотров: 339; Мы поможем в написании вашей работы!; Нарушение авторских прав |