Аксиоматическое построение теории вероятностей.

Развитие естествознания в начале текущего столетия предъявило к теории вероятностей повышенные требования. Возникла необходимость в систематическом изучении основных понятий теории вероятностей и выяснении тех условий, при которых возможно ис­пользование ее результатов. Вот почему особенно важное значение приобрело формально-логическое обоснование теории вероятностей, ее аксиоматическое построение. При этом в основу теории вероятностей как математической науки должны быть положены некоторые предпосылки, являющиеся обобщением многовекового человеческого опыта. Теория вероятностей должна строиться из аксиом так же, как любая сформировавшаяся математическая наука—алгебра, геометрия, абстрактная теория групп и т.д.

В современной математике принято аксиомами называть те предложения, которые принимаются за истинные и в пределах данной теории не доказываются. Все остальные положения этой теории должны выводиться чисто логическим путем из принятых аксиом. Формулировка аксиом, т. е. тех фундаментальных положений, на базе которых строится обширная теория, представляет собой не начальную стадию развития математической науки, а является результатом длительного накопления фактов и логического анализа полученных результатов с целью выявления действительно основных первичных фактов. Впервые задача аксиоматического построения теории вероятностей как логически совершенной науки была поставлена и решена в 1917 г. известным математиком С. Н. Бернштейном. При этом С. Н. Бернштейн исходил из качественного сравнения случайных событий по их большей или меньшей вероятности.

Имеется иной подход, предложенный А. Н. Колмогоровым, который тесно связывает теорию вероятностей с современной метрической теорией функций, теорией множеств.

Аксиоматическое построение основ теории вероятностей отправляется от основных свойств вероятности, подмеченных на примерах классического и статистического определений.

В аксиоматике теории вероятностей Колмогорова понятие случайного события не является первичным, а строится из более элементарных понятий. С таким подходом мы уже встречались при рассмотрении некоторых примеров. Так, в задачах на геометрическое определение вероятности рассматривается область G пространства (прямой, пло­скости и т.д.), в которую «наудачу» бросается точка. Случайными событиями при этом являются попадания в те или иные подобласти области G. Каждое случайное событие является при этом некоторым подмножеством множества точек G. Эта мысль положена в основу общей концепции случайного события в аксиоматике А. Н. Колмогорова.

Колмогоров исходит из множества (пространства) U элементарных событий. Что представляют собой элементы этого множества для логического развития теории вероятностей — безразлично.

Далее рассматривается некоторая система F подмножеств множества U', элементы системы F называются случайными событиями.

Относительно структуры системы F предполагаются выполненными три следующих требования:

1) F в качестве элемента содержит множество U.

2) Если А и В—подмножества множества U—входят в F в качестве элементов, то в качестве элементов F содержит также множества А+В, АВ, А–В и т.д.

Второе требование влечет за собой принадлежность к множеству F сумм, произведений и дополнений конеч­ного числа событий, принадлежащих F. Таким образом, элементарные операции над случайными событиями не могут вывести нас за пределы множества случайных событий. Назовем систему событий F полем событий.

Во многих важнейших задачах нам понадобится от поля событий требовать большего, а именно

3) Если подмножества 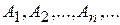множества U являются элементами множества F, то их сумма 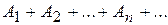и произведение также являются элементами F.

Множество F, образованное описанным способом, носит название борелевского поля событий.

Только что изложенный способ определения случайного события вполне согласуется с тем представлением, которое мы получили при рассмотрении конкретных примеров. Для большей ясности рассмотрим пример.

Пример 1. Бросается игральная кость. Множество U элементарных событий состоит из шести элементов: . Здесь 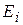означает выпадение i очков. Множество F случайных событий состоит из следующих 2⁶ = 64 элементов:

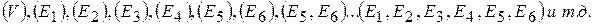
Здесь каждая скобка показывает, из каких элементов множества U составлено подмножество, входящее в качестве элемента в состав F символом (V) мы обозначили пустое множество.

Определение 1. Если два случайных события А и В не имеют в своем составе одних и тех же элементов множества U, то мы будем называть их несовместимыми.

Событие U будем называть достоверным событием, а событие V (пустое множество) — невозможным событием. События 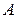и 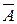называются противоположными.

Теперь мы можем перейти к формулировке аксиом, определяющих вероятность.

Аксиома 1. Каждому случайному событию 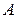из поля событий F поставлено в соответствие неотрицательное число Р(A), называемое его вероятностью.

Аксиома 2. Р (U)=1.

Аксиома 3(аксиома сложения). Если события 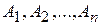попарно несовместимы, то

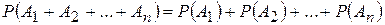
(1.6.1)

Для классического определения вероятности свойства, выраженные аксиомами 2 и 3, не нужно было постулировать, так как эти свойства вероятности были нами доказаны. Утверждение же аксиомы 1 содержится в самом классическом определении вероятности.

Из сформулированных аксиом мы выведем несколько важных элементарных следствий.

1. Вероятность невозможного события равна нулю.

Из равенства 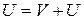и аксиомы 3 мы заключаем, что .

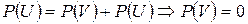2. Для любого события A: .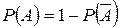

Так как , 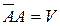тогда 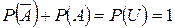откуда .

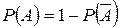3. Каково бы ни было случайное событие A, .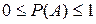

4. Если событие A влечет за собой событие В, то .

5. Пусть A и В — два произвольных события. Поскольку в суммах 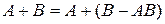и 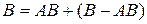слагаемые являются несовместимыми событиями, то в соответствии с аксиомой 3

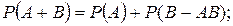
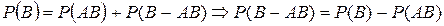
Отсюда вытекает теорема сложения для произвольных событий A и B 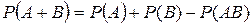. В силу не отрицательности 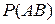отсюда заключаем, что .

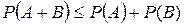По индукции теперь выводим, что если - произ­вольные события, то имеет место неравенство

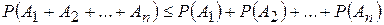
(1.6.2)

Система аксиом Колмогорова непротиворечива, так как сущест­вуют реальные объекты, которые всем этим аксиомам удовлетворяют. Например, если за U принять произвольное множество с конечным числом элементов 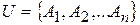, за F —совокупность всех подмножеств 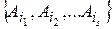, , 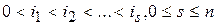то, положив

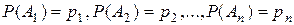
(1.6.3)

где 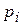— произвольные неотрицательные числа, удовле­творяющие равенству .

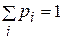Система аксиом Колмогорова неполна: даже для одного и того же множества U вероятности в множестве F мы можем выбирать раз­личными способами.

Так, в рассмотренном нами примере с игральной костью мы можем положить или

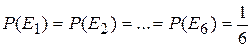
или

Неполнота системы аксиом теории вероятностей не является сви­детельством их неудачного выбора или недостаточной работы мысли при их создании.

Дальнейшее развитие теории нуждается в дополнительном пред­положении, которое носит название расширенной аксиомы сложе­ния. Необходимость введения новой аксиомы объясняется тем, что в теории вероятностей постоянно приходится рассматривать события, подразделяющиеся на бесконечное число частных случаев.

Расширенная аксиома сложения. Если событие А равносильно наступлению хотя бы одного из попарно несовме­стимых событий 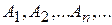, то

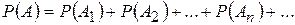
(1.6.4)

Заметим, что расширенная аксиома сложения может быть заме­нена равносильной ей аксиомой непрерывности.

Аксиома непрерывности. Если последовательность событий 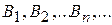такова, что каждое последующее влечет за собой предыдущее и произведение всех событий 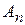есть невозможное событие, то

(1.6.5)

Докажем эквивалентность только что сформулированных предло­жений.

1. Из расширенной аксиомы сложения следует аксиома непре­рывности. Действительно, пусть события 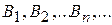та­ковы, что 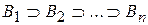и при любом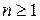

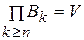
(1.6.6)

Очевидно, что

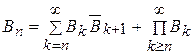
(1.6.7)

Так как события, стоящие в этой сумме, попарно несовместимы, то согласно расширенной аксиоме сложения

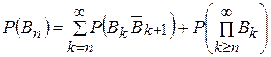
(1.6.8)

Но в силу условия (1.6.6)

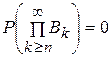
(1.6.9)

поэтому

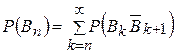
(1.6.10)

т. е. 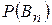есть остаток сходящегося ряда

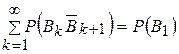
(1.6.11)

Поэтому .

2. Из аксиомы непрерывности следует расширенная аксиома сло­жения. Пусть события ... попарно несовместимы и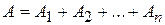

Положим

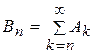
(1.6.12)

Ясно, что 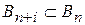. Если событие 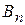наступило, то наступило ка­кое-нибудь из событий 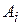и, значит, в силу по парной несо­вместимости событий 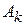события 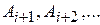уже не наступили. Таким образом, события 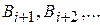невозможны и, следовательно, невозможно событие 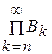. По аксиоме непрерывности .

Так как 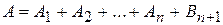, то по обычной аксиоме сложения

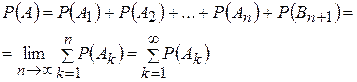
(1.6.13)

В заключение мы можем сказать, что с точки зрения теории мно­жеств данное нами аксиоматическое определение вероятности есть не что иное, как введение в множестве U нормированной, счетно-адди­тивной, неотрицательной меры P, определенной для всех элементов множества F.

При определении понятия вероятности мы должны указывать не только исходное множество элементарных событий U (в современных работах его часто обозначают также буквой Q), но также множество случайных событий F и определенную на нем функцию Р. Совокупность [U,F,Р] называется вероятностным пространством.