
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Геометрические вероятности.
Еще в самом начале развития теории вероятностей была замечена недостаточность «классического» определения вероятности, основанного на рассмотрении конечной группы равновероятных событий. Уже тогда частные примеры привели к некоторому видоизменению этого определения и построению понятия вероятности также для случаев, когда мыслимо бесконечное множество исходов. При этом по-прежнему основную роль играло понятие «равновероятности» некоторых событий.
Общая задача, которая ставилась и привела к расширению понятия вероятности, может быть сформулирована следующим способом.
Пусть, например, на плоскости имеется некоторая область G и в ней содержится другая область g с квадрируемой границей. В область G наудачу бросается точка и спрашивается, чему равна вероятность того, что точка попадет в область g. При этом выражению «точка бросается наудачу в область G» придается следующий смысл: брошенная точка может попасть в любую точку области G, вероятность попасть в какую-либо часть области G пропорциональна мере этой части (длине, площади и т. д.) и не зависит от ее расположения и формы.
Таким образом, по определению, вероятность попадания в область g при бросании наудачу точки в область G равна

| (1.4.1) |
Рассмотрим несколько примеров.
Пример 1. Задача о встрече. Два лица А и В условились Встретиться в определенном месте между 12 часами и часом. Пришедший первым ждет другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц А и В, если приход каждого из них в течение указанного часа может произойти наудачу и моменты прихода независимы.
Решение. Обозначим моменты прихода лица А через х и лица В через у. Для того чтобы встреча произошла, необходимо и достаточно, чтобы  .
.
Будем изображать хOу как декартовы координаты на плоскости; в качестве единицы масштаба выберем минуту. Всевозможные исходы изобразятся точками квадрата со сторонами 60; благоприятствующие

встрече — расположатся в заштрихованной области (рис. 1.4.1).
Искомая вероятность равна отношению площади заштрихованной фигуры к площади всего квадрата:  .
.
Пример 3. Задача Бюффона. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу бросается игла длины 2l(l≤a). Найти вероятность того, что игла пересечет какую-нибудь прямую.
Решение. Обозначим через х расстояние от центра до ближайшей параллели и через  —угол, составленный иглой с этой параллелью. Величины х и
—угол, составленный иглой с этой параллелью. Величины х и  полностью определяют положение иглы. Всевозможные положения иглы определяются точками прямоугольника со сторонами a и
полностью определяют положение иглы. Всевозможные положения иглы определяются точками прямоугольника со сторонами a и  . Из рис. 1.4.2. видно, что для пересечения иглы с параллелью необходимо и достаточно, чтобы
. Из рис. 1.4.2. видно, что для пересечения иглы с параллелью необходимо и достаточно, чтобы  .
.
Искомая вероятность в силу сделанных предположений равна отношению площади заштрихованной на рис. 1.4.3. области к площади прямоугольника
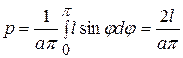
|
Заметим, что задача Бюффона являлась исходным пунктом для решения некоторых проблем теории стрельбы, учитывающих размеры снаряда.

Полученная формула была использована для опытного определения приближенного значения числа  . Таких опытов с бросанием иглы было проведено довольно много. Мы приведем результаты лишь некоторых из них(см. Табл. 1.4.1).
. Таких опытов с бросанием иглы было проведено довольно много. Мы приведем результаты лишь некоторых из них(см. Табл. 1.4.1).
Табл. 1.4.1
| Экспериментатор | Год | Число бросков иглы | Экспериментальное значение |
| Вольф | 3,1596 | ||
| Смит | 3,1553 | ||
| Фокс | 3,1419 |
Так как из полученной нами формулы следует равенство  , то при большом числе бросаний п приближенно
, то при большом числе бросаний п приближенно  , где т — число происшедших при этом пересечений.
, где т — число происшедших при этом пересечений.
Дата добавления: 2014-12-23; просмотров: 446; Мы поможем в написании вашей работы!; Нарушение авторских прав |