Числовые характеристики случайных величин.

Наиболее полная вероятностная характеристика поведения случайной величины определяется функцией распределения. Однако в ряде случаев не требуется столь полная ее вероятностная характеристика, а необходимо знать лишь некоторые фрагменты ее вероятностного поведения. В теории вероятностей и ее приложениях для характеристики поведения случайных величин используют некоторые постоянные величины, получаемые по определенным правилам. Среди них особенно важны математическое ожидание, дисперсия и моменты различных порядков. С их помощью допускается решение многих вероятностных задач.

1. Математическое ожидание. Среди характеристик случайных величин прежде всего отметим характеристику положения случайной величины на числовой прямой, то есть укажем некоторое число(значение) вокруг которого группируются все возможные значения случайной величины.

Рассмотрим следующий пример. Пусть при стрельбе из некоторого орудия для поражения цели требуется один снаряд с вероятностью , два снаряда – с вероятностью p₂ , три снаряда - с вероятностью p₃ …, n снарядов - с вероятностью p_n. Известно что при стрельбе цель будет поражена. Спрашивается сколько снарядов в среднем потребуется для поражения цели.

Итак, известно, что

Тогда

Пусть - возможные значения случайной величины Х, а - соответствующие им вероятности.

Определение 1. Если ряд (или ) сходится абсолютно, то есть (или ), то его сумма называется математическим ожиданием случайной величины Х и обозначается М[X] или Е[X].

Для непрерывных случайных величин естественным будет следующее обобщение:

Определение 2. Пусть Х – непрерывная случайная величина и f(x) – ее плотность распределения, то математическим ожиданием случайной величины Х называется интеграл , если он сходится абсолютно, то есть когда существует интеграл .

Часто математическое ожидание обозначают символом .

Математическое ожидание существует не для любой случайной величины. Пусть Х дискретная случайная величина, имеющая ряд распределения представленный в табл. 3.4.1.

Табл.3.4.1

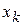
	2	22	…	2k
			…

то есть данный ряд есть ряд распределения случайной величины Х. Определим математическое ожидание случайной величины Х, , так как ряд расходится, то математическое ожидание не существует.

Кроме математического ожидания на практике применяются и другие характеристики положения, в частности мода и медиана.

2.Мода. Определение 3. Модой случайной величины Х называется наиболее вероятное ее значение. Термин «наиболее вероятное значение», строго говоря, применим только к дискретной случайной величине, для непрерывных случайных величин модой является то значение, при котором плотность вероятности достигает наибольшего значения. Условимся обозначать моду символом М₀ .

Если кривая распределения(многоугольник) имеет более одного максимума, то распределение называется полимодальным, если распределение имеет минимум, то оно называется «антимодальным».

3.Медиана. Определение 4. Медианой случайной величины Х называется такое число М_е на числовой прямой, для которого справедливо следующее равенство: , то есть одинаково вероятны, события состоящие в том, что случайная величина Х окажется меньше или больше чем число М_е.

Медиана это абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам. В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.

4. Моменты, дисперсия, среднеквадратическое отклонение. В теории вероятностей употребляется ряд характеристик, которые описывают различные свойства распределения случайных величин. Наиболее важными понятиями являются понятия начальных и центральных моментов.

Определение 5. Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-той степени данной случайной величины, то есть

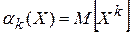
(3.4.1)

Для дискретной случайной величины начальный момент k-го порядка определяется формулой , а для непрерывной случайной величины с плотностью распределения f(x) соответственно .

Не трудно заметить, что первый начальный момент есть математическое ожидание случайной величины.

Определение 6. Центрированной случайной величиной , соответствующей случайной величине Х будем называть величину, определяемую равенством =Х-m_x. Заметим, что

Определение 7. Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-той степени центрированной случайной величины :

(3.4.2)

Формулы для вычисления центральных моментов имеют вид:

для дискретной случайной величины Х:

для непрерывной случайной величины Х:

Полезно отметить, что для дискретной случайной величины Х может быть вычислен по следующей формуле:

Аналогичную формулу можно получить для непрерывной случайной величины Х.

Ввиду крайней важности второй центральный момент называют дисперсией случайной величины. Дисперсия случайной величины есть характеристика рассеяния(разбросанности) значений случайной величины относительно m_x . Для дисперсии вводят специальное обозначение:

(3.4.3)

Определение 8. Дисперсией случайной величины Х называется математическое ожидание квадрата соответствующей центрированной случайной величины.

Дисперсия имеет размерность квадрата случайной величины Х. Поэтому часто для наглядности решения задачи пользуются величиной размерность, которой совпадает с Х. Ее называют среднеквадратическим отклонением и определяют по следующей формуле

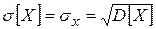
(3.4.4)

5. Коэффициент асимметрии (скошенности). Характеризует смещение распределения случайной величины Х относительно математического ожидания

(3.4.5)

- m_x смещено вправо или распределение смещено влево относительно математического ожидания m₁.

- m_x смещено влево или распределение смещено вправо относительно математического ожидания m₂.

Для симметричных законов .

6. Эксцес. Характеризует островершинность или туповершинность кривой распределения. Определяется соотношением

(3.4.6)

Для гаусовского(I) распределения Е_х=0.

Е_х>0–островершинность(II)

Е_х<0–туповершинность(III)

Простейшие свойства основных числовых характеристик.

1) 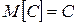Доказательство .

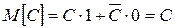2) Доказательство приведем для непрерывной случайной величины .

3) , так как .

7. Квантили.

Определение 9. Квантилью x_p уровня 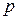случайной величины Х называется решение уравнения .

Это определение абсолютно корректно для случайных величин со строго монотонной функцией 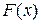(рис. 3.4.6.а) и требует уточнений для случая, когда решением уравнения является целый промежуток (рис. 3.4.6.б). В последнем случае введение квантили вопрос договорённости. Мы будем считать, что .

Для случая непрерывной случайной величины можно дать другое геометрическое толкование квантили : это такая точка на оси абсцисс, левее которой график плотности распределения ограничивает площадь, численно равную 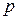(рис 3.4.7)

Рис 3.4.7. Геометрическая интерпретация для функции

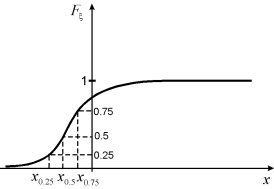
Рис 3.4.8. Медиана, верхняя и нижняя квартили распределения для функци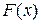й и

Наиболее часто встречаются квантили уровней (медиана распределения), (нижняя квартиль) и (верхняя квартиль). Эти квантили делят числовую прямую на 4 части, вероятность попадания в которые равна (см. рис. 3.4.8).

Использование квантилей распределений широко применяется в задачах математической статистики.