Биномиальное распределение.

Рассмотрим дискретную случайную величину Х , которая принимает значения 0,1,2,…n с вероятностями

(4.1.1)

В схеме Бернулли: Х – число наступлений m раз события А в серии из n – независимых испытаний. Введем в рассмотрение производящую функцию, которая в данном случае имеет вид

(4.1.2)

Нетрудно заметить, что .

Придавая значение Z=1, получим

(4.1.3)

Подсчитаем числовые характеристики биномиального распределения:

1) математическое ожидание в соответствии с определением выражается формулой:

(4.1.4)

Найдем производную производящей функции:

(4.1.5)

Придавая значение Z=1, получим

(4.1.6)

Из соотношения (4.1.6) следует

(4.1.7)

Далее подсчитаем дисперсию 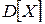по формуле 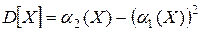. Второй начальный момент определяется формулой

(4.1.5)

Умножим производную производящей функции на z:

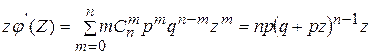
Дифференцируя полученное выражение, получим

и вычисляя при Z=1, получим

(4.1.6)

Из (4.1.6) нетрудно заметить, что , тогда:

	(4.1.7)
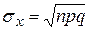
	(4.1.8)

Если р–мало, а п–достаточно большое число, то формулой биномиального распределения пользоваться не удобно.