
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функция распределения системы двух случайных величин.
Функцией распределения системы двух случайных величин (X,Y) называется вероятность совместного выполнения двух неравенств X<х и Y<у:

| (5.2.1) |
Если пользоваться для геометрической интерпретации системы образом случайной точки (случайного вектора), то функция распределения F(х,у) есть не что иное, как вероятность попадания случайной точки (X,Y) в бесконечный квадрант с вершиной в точке (х,у), лежащий левее и ниже ее (рис. 5.2.1).
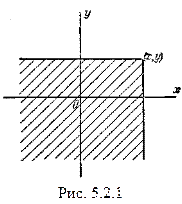
Сформулируем свойства функции распределения системы случайных величин.
1. Функция распределения F(x,у) есть неубывающая функция обоих своих аргументов, т. е.
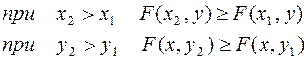
В этом свойстве функции F(х) можно наглядно убедиться, пользуясь геометрической интерпретацией функции распределения как вероятности попадания в квадрант с вершиной (х,у) (рис. 5.2.1). Действительно, увеличивая х (смещая правую границу квадранта вправо) или увеличивая у (смещая верхнюю границу вверх), мы, очевидно, не можем уменьшить вероятность попадания в этот квадрант.
2. Повсюду на  функция распределения равна нулю:
функция распределения равна нулю:
F(x, 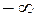 ) = F(
) = F( 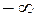 , y) = F(
, y) = F( 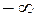 ,
, 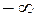 ) = 0.
) = 0.
В этом свойстве мы наглядно убеждаемся, неограниченно отодвигая влево правую границу квадранта (x  ) или вниз его верхнюю границу (у
) или вниз его верхнюю границу (у 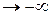 ) или делая это одновременно с обеими границами; при этом вероятность попадания в квадрант стремится к нулю.
) или делая это одновременно с обеими границами; при этом вероятность попадания в квадрант стремится к нулю.
3. При одном из аргументов, равном 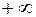 , функция распределения системы превращается в маргинальную функцию распределения случайной величины, соответствующей другому аргументу:
, функция распределения системы превращается в маргинальную функцию распределения случайной величины, соответствующей другому аргументу:
F (x, 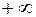 ) = Fl (x), F (
) = Fl (x), F ( 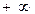 , у) = F2 (у),
, у) = F2 (у),
где F1(x), F2(y) — соответственно маргинальные функции распределения случайных величин X и Y.
4. Если оба аргумента равны 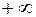 , функция распределения системы равна единице:
, функция распределения системы равна единице:
F(  ,
,  ) = 1
) = 1
Действительно, при x 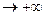 , y
, y 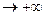 квадрант с вершиной (х,у) в пределе обращается во всю плоскость хОу, попадание в которую есть достоверное событие.
квадрант с вершиной (х,у) в пределе обращается во всю плоскость хОу, попадание в которую есть достоверное событие.
Условимся событие, состоящее в попадании случайной точки (X, Y) в область D, обозначать символом (X, Y)  D.
D.
Вероятность попадания случайной точки в заданную область выражается наиболее просто в том случае, когда эта область представляет собой прямоугольник со сторонами, параллельными координатным осям.
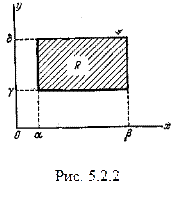
Выразим через функцию распределения системы вероятность попадания случайной точки (X, Y) в прямоугольник R, ограниченный абсциссами 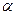 и
и  ординатами
ординатами  и
и  (рис. 5.2.2).
(рис. 5.2.2).
Тогда событие (X,Y)  R будет равносильно произведению двух событий:
R будет равносильно произведению двух событий: 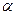
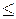 Х
Х 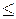
 и
и 
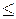 Х
Х 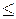
 . Выразим вероятность этого события через
. Выразим вероятность этого события через

функцию распределения системы. Для этого рассмотрим на плоскости хОу четыре бесконечных квадранта с вершинами в точках  рис. 5.2.3.
рис. 5.2.3.
Очевидно, вероятность попадания в прямоугольник R равна вероятности попадания в квадрант  минус вероятность попадания в квадрант
минус вероятность попадания в квадрант 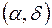 минус вероятность попадания в квадрант
минус вероятность попадания в квадрант 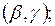 плюс вероятность попадания в квадрант
плюс вероятность попадания в квадрант  (так как мы дважды вычли вероятность попадания в этот квадрант). Отсюда получаем формулу, выражающую вероятность попадания в прямоугольник через функцию распределения системы:
(так как мы дважды вычли вероятность попадания в этот квадрант). Отсюда получаем формулу, выражающую вероятность попадания в прямоугольник через функцию распределения системы:

| (5.2.2) |
Дата добавления: 2014-12-23; просмотров: 411; Мы поможем в написании вашей работы!; Нарушение авторских прав |