Плотность распределения системы двух случайных величин.

Важное практическое значение имеют системы непрерывных случайных величин(непрерывные случайные векторы).

Пусть имеется система двух непре­рывных случайных величин (X, Y), которая интерпретируется случайной точкой на плоскости хОу. Рассмотрим на этой плоскости малый прямоугольник со сторонами и , примыкающий к точке с координатами (х,у) (рис. 5.3.1). Вероятность попадания в этот прямоугольник равна

Разделим вероятность попадания в прямоугольник на площадь этого прямоугольника и перейдем к пределу при и :

Предположим, что функция F(x, у) не только непрерывна, но и дифференцируема; тогда правая часть формулы представляет собой вторую смешанную частную производную функции F(x, у) по х и у. Обозначим эту производную f(x, у):

(5.3.1)

Функция f(х,у) называется плотностью совместного распределения системы.

Геометрически функцию f(x,у) можно изобразить некоторой поверхностью (рис. 5.3.2). Эта поверхность аналогична кривой распределения для одной случайной ве­личины и называется поверхностью распределения.

Если пересечь поверхность рас­пределения f(х,у) плоскостью, па­раллельной плоскости хОу, и спроек­тировать полученное сечение на плоскость хОу, получится кривая, в каждой точке которой плотность распределения постоянна. Такие кривые называются кривыми равной плотности. Кривые равной плот­ности, очевидно, представляют собой горизонтали поверхности распределения.

Рассматривая плотность распределения f(х) для одной случайной величины, мы ввели понятие «элемента вероятности» f(x)dx.. Аналогичное понятие «элемента вероятности» вводится и для системы двух случайных величин. Элементом вероятности в данном случае называется выражение

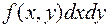
(5.3.2)

Очевидно, элемент вероятности есть не что иное, как вероятность попадания в элементарный прямоугольник со сторонами dx,dy, примыкающий к точке (х,у) (рис. 5.3.1). Эта вероятность равна объему элементарного параллелепипеда, ограниченного сверху поверхностью f(x,у) и опи­рающегося на элементарный прямоугольник dx dy (рис. 5.3.3).

Пользуясь понятием элемента вероятности, выведем выражение для вероятности попадания случайной точки в произвольную область D. Эта вероятность, очевидно, может быть получена суммированием (интегрированием) элементов вероятности по всей области D:

(5.3.3)

Геометрически вероятность попадания в область D изображается объемом цилиндрического тела С, ограниченного сверху поверхностью распределения и опирающегося на область D (рис. 5.3.4).

Из обшей формулы (5.3.3) вытекает формула для вероятности попадания в прямоугольник R, ограниченный абсциссами и и ординатами и (5.2.2):

Функция распределения F(x,у) есть вероятность попадания в бесконечный квадрант; последний можно рассматривать как прямо­угольник, ограниченный абсциссами и х и ординатами и у.

Легко убедиться в следующих свойствах плотности распределения системы:

1. Плотность распределения системы есть функция неотрица­тельная:

Это ясно из того, что функция распределения является неубывающей функцией своих аргументов.

2. Двойной интеграл в бесконечных пределах от плотности рас­пределения системы равен единице: