Теорема Лапласа.

Если - число появлений случайного события А в п независимых повторных испытаниях с исходами , вероятности которых , то

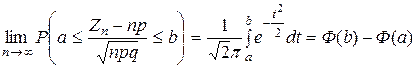
(10.3.1)

Доказательство. Пусть - число появлений события А в i-м независимом повторном испытании в серии из п испытаний. Очевидно это - дискретная случайная величина с рядом распределения:

где .

Очевидно, существуют

	(10.3.2)

В силу независимости испытаний случайные величины 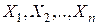можно считать независимыми.

Таким образом, для рассматриваемых здесь случайных величин выполняются все условия теоремы Ляпунова.

Следовательно, имеет место соотношение (10.2.2).

Случайную величину в выражении (10.2.2) в рассматриваемом случае можно представить в виде

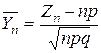
(10.3.3)

где

при условии независимости случайных величин .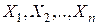

Таким образом, доказано, что если выполнены условия теоремы Лапласа, то

Отсюда, учитывая определение стандартного нормального закона , находим, что соотношение (10.3.1) справедливо.