Краткая теоретическая часть. Классическое определение вероятности сводит понятие вероятности к понятию равновероятности (равновозможности) событий

Классическое определение вероятности сводит понятие вероятности к понятию равновероятности (равновозможности) событий, которое считается основным и не подлежит формальному определению. Для примера: при бросании кубика, который имеет точную форму куба и изготовлен из вполне однородного материала, равновероятными событиями будут выпадения какого-нибудь определенного числа очков (1,2,3,4,5,6), обозначенного на гранях этого куба, поскольку в силу наличия симметрии ни одна из граней не имеет объективного преимущества перед другими.

В общем случае рассмотрим какую-либо группу G, состоящую из n попарно несовместимых равновозможных событий (назовем их элементарными событиями): .

Образуем теперь систему F, состоящую из невозможного события V, всех событий E_k группы G и всех событий А,B,С… которые мо­гут быть подразделены на частные случаи, входящие в состав группы G.

Например, если группа G состоит из трех событий 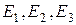, то в систему F входят события V, E₁,E₂,E₃,E₁+E₂, E₂+E₃, E₁+E₃,U=E₁+E₂+E₃. и т.д.

Легко установить, что система F есть поле событий. В самом деле, очевидно, что сумма, разность и произведение событий из F входят в F; невозможное событие V входит в F по определению, а достоверное событие U входит в F, так как оно представляется в виде

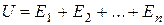
Классическое определение вероятности дается для событий системы F и может быть сформулировано так:

Если событие А подразделяется на т частных случаев, входящих в полную группу из n попарно несовместимых и равновозможных событий, то вероятность Р(A) события А равна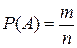

Например, при однократном бросании игральной кости полная группа попарно несовместимых и равновероятных событий состоит из событий 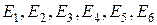, которые состоят соответственно в выпадении 1,2,3,4,5,6 очков. Событие 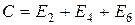, состоящее в выпадении четного числа очков, подразделяется на три частных случая, входящих в состав полной группы несовместимых и равновероятных событий. Поэтому вероятность события С равна .

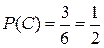Очевидно также, что в силу принятого определения

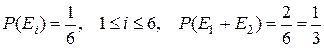и т. д.

В теории вероятностей широко используется следующая термино­логия, к которой мы часто впоследствии будем обращаться. Представим себе, что для выяснения вопроса, произойдет или не произойдет событие А (например, выпадение числа очков, кратного трем), необходимо произвести некоторое испытание (т. е. осуществить комплекс условий), которое дало бы ответ на поставленный вопрос (в нашем примере требуется бросить игральную кость). Полная группа попарно несовместимых и равновероятных событий, которые могут произойти при таком испытании, называется полной группой возможных результатов испытания. Те из возможных результатов испытания, на которые подразделяется событие А, называются результатами испытания, благоприятствующими А. Пользуясь этой терминологией, можно сказать, что вероятность Р(A) события А равняется отношению числа возможных результатов испытания, благоприятствующих событию А, к числу всех возможных результатов испытания.

Тест.

1. Какие из приведенных событий не являются элементарными? Укажите два события.

а) Выпадение определенной грани при подбрасывании игральной кости

б) Извлечение белого шара из урны, содержащей белые и черные шары

в) Выпадение четного числа очков при подбрасывании кубика

г) Извлечение карты определенной масти из колоды

д) Попадание баскетболистом в кольцо5

2. Какие из приведенных событий являются равновозможными? Укажите три события.

а) Выпадение четного и нечетного числа очков при подбрасывании кубика

б) Попадание охотником в медведя или зайца

в) Прием на руководящую должность женщины и мужчины по Конституции РФ

г) Выпадение герба и цифры при подбрасывании монетки

д) Успешная сдача экзамена по теории вероятностей студентом-отличником и студентом-троечником

е) Извлечение внучкой из корзинки бабушки наудачу яблока и груши, если в ней лежал 1 кг яблок и 2 кг груш

3. Группу событий называют полной, если:

а) ни одно из них не произойдет в ходе опыта

б) ровно одно из них произойдет в ходе опыта

в) по крайней мере одно из них произойдет в ходе опыта

г) каждое из них произойдет в ходе опыта

4. В каких случаях применимо классическое определение вероятности?

а) Если результат опыта можно представить как сумму несовместных элементарных событий

б) Если результат опыта можно представить как сумму равновозможных элементарных событий

в) Если результат опыта можно представить как сумму противоположных элементарных событий

г) Если результат опыта можно представить как полную группу попарно несовместных и равновозможных элементарных событий

д) Если результат опыта можно представить как полную группу равновозможных элементарных событий

5. Пусть n – число всех возможных исходов испытания, а m - число благоприятствующих исходов появлению события А исходов. Какой вид будет иметь формула непосредственного подсчета вероятности события А?

а) P =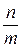

б) P =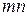

в) P =

г) P =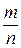

д) P =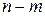

6. Можно ли использовать классическое определение вероятности, если число исходов испытания бесконечно?

а) Да

б) Нет