
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение типовых задач. Пример 2.1. На горизонтальной плоскости вдоль прямой АВ через интервал l расположены оси одинаковых вертикальных цилиндров с радиусом основания г
Пример 2.1. На горизонтальной плоскости вдоль прямой АВ через интервал l расположены оси одинаковых вертикальных цилиндров с радиусом основания г. Под углом q к прямой бросается шар радиуса R. Определить вероятность столкновения шара с цилиндром, если пересечение линии движения центра шара с прямой АВ равновозможное в любой точке.
Решение.
Введем в рассмотрение событие А, состоящее в том, что произойдет столкновение шара с цилиндром. Пусть х — расстояние от центра шара до ближайшей линии, проходящей через центр цилиндра параллельно направлению перемещения центра шара. Возможные значения x определяются условиями (рис.1):


Столкновение шара с цилиндром произойдет в том случае, если  .
.
Искомая вероятность равна отношению длин отрезков, на которых находятся благоприятствующие и все возможные значения x.
Поэтому

Пример 2.2. На одной дорожке магнитофонной ленты длиной 200 м записано сообщение на интервале 20 м, на второй — записано аналогичное сообщение. Определить вероятность того, что в интервале от 60 до 85 м не будет промежутка ленты, не содержащего записи, если начала обоих сообщений равновозможные в любой точке от 0 до 180 м.
Решение.
Введем в рассмотрение событие А, состоящее в том, что в интервале от 60 до 85 м не будет промежутка ленты, не содержащего записи. Пусть x и у — координаты начала записей, причем  . Так как
. Так как  , то областью возможных значений x и у является, треугольник с катетами по 180 м. Площадь этого треугольника
, то областью возможных значений x и у является, треугольник с катетами по 180 м. Площадь этого треугольника  .
.
Найдем область значений x и у, благоприятствующих указанному событию. Для того чтобы получилась непрерывная запись, необходимо выполнение неравенства  . Чтобы интервал записи был не менее 25 м, должно быть
. Чтобы интервал записи был не менее 25 м, должно быть  . Кроме того, для получения непрерывной записи на интервале от 60 до 85м должно быть
. Кроме того, для получения непрерывной записи на интервале от 60 до 85м должно быть  ,
, 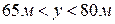 .
.
 Проведя границы указанных областей, получим, что благоприятствующие значения x и y заключены в треугольнике, площадь которого
Проведя границы указанных областей, получим, что благоприятствующие значения x и y заключены в треугольнике, площадь которого  (рис. 2). Искомая вероятность равна отношению площади SБ, попадание в которую благоприятствует данному событию, к площади области S возможных значений x и у, т. е.
(рис. 2). Искомая вероятность равна отношению площади SБ, попадание в которую благоприятствует данному событию, к площади области S возможных значений x и у, т. е. 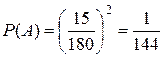 .
.
Пример 2.3. В любые моменты промежутка времени Т равновозможны поступления в приемник двух сигналов. Приемник будет забит, если разность между моментами поступления сигналов будет меньше  . Определить вероятность того, что приемник будет забит.
. Определить вероятность того, что приемник будет забит.
Решение.
 Введем в рассмотрение событие А, состоящее в том, что приемник будет забит.
Введем в рассмотрение событие А, состоящее в том, что приемник будет забит.
Пусть x и у — моменты поступления сигналов в приемник.
Областью возможных значений x, у является квадрат площадью T2 (рис. 3). Приемник будет забит, если  . Данная область лежит между прямыми
. Данная область лежит между прямыми  и
и  .
.
Ее площадь  , поэтому
, поэтому  .
.
Пример 2.4. Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше единицы, не превзойдет единицы, а их произведение будет не больше 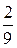 ?
?
Решение.
Введем в рассмотрение событие А, состоящее в том, что сумма двух наугад взятых положительных чисел, каждое из которых не больше единицы, не превзойдет единицы, а их произведение будет не больше 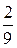 . Пусть x и у — взятые числа. Их возможные значения
. Пусть x и у — взятые числа. Их возможные значения  ,
,  , что на плоскости соответствует квадрату с площадью S=1. Благоприятствующие значения удовлетворяют условиям:
, что на плоскости соответствует квадрату с площадью S=1. Благоприятствующие значения удовлетворяют условиям:  и
и  .
.
 Граница
Граница  делит квадрат пополам, причем область
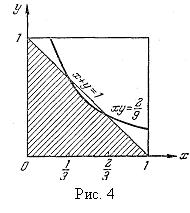
делит квадрат пополам, причем область  представляет собой нижний треугольник (рис. 4).
представляет собой нижний треугольник (рис. 4).
Вторая граница  является гиперболой. Абсциссы точек пересечения этих границ:
является гиперболой. Абсциссы точек пересечения этих границ:  и
и  . Величина благоприятствующей площади
. Величина благоприятствующей площади 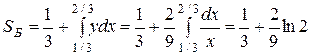 . Искомая вероятность
. Искомая вероятность  .
.
Дата добавления: 2014-12-23; просмотров: 1760; Мы поможем в написании вашей работы!; Нарушение авторских прав |