
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Занятие 4. Теорема сложения вероятностей.
Краткая теоретическая часть
Вероятность суммы двух событий определяется по формуле
P(A+В) = Р(A)+Р(B) — Р(AB),
которая обобщается на сумму любого числа событий
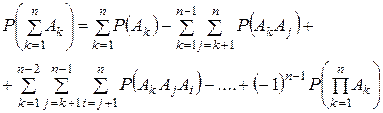
Для несовместных событий вероятность суммы событий равна сумме вероятностей этих событий, т. е.  .
.
Тест
1. В каком случае события А и В называются несовместными или несовместимыми?
а) Когда вероятность появления одного из них не зависит от вероятности появления второго
б) Когда хотя бы одно из этих событий произойдет в ходе испытания
в) Когда совместное появление этих событий невозможно
г) Когда оба этих события произойдут в ходе опыта
2. Укажите события, которые являются совместимыми.
а) Выпадение «герба» и цифры при подбрасывании монеты
б) Присутствие одного и того же студента одновременно на лекции в аудитории и в кинотеатре
в) Наступление весны по календарю и выпадение снега
г) Появление на выпавшей грани каждой из двух игральных костей трех очков и равенство суммы очков на выпавших гранях обеих костей нечетному числу
д) Показ по одному каналу телевидения футбольного матча, а по другому – выпуска новостей
3. Теорема сложения вероятностей несовместных событий формулируется следующим образом:
а) Вероятность появления одного из двух несовместных событий равна вероятности появления второго события 
б) Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий 
в) Вероятность появления одного из двух несовместных событий равна разности вероятностей появления этих событий 
4. Теорема сложения вероятностей совместных событий формулируется следующим образом:
а) Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий 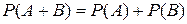
б) Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления 
в) Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий и вероятности их совместного появления 
5. Теорема сложения вероятностей обобщается на сумму любого числа событий и вероятность суммы событий в общем виде вычисляется по формуле:
а) 
б) 
в) 
6. Если события  ,
,  являются несовместными, то вероятность суммы этих событий равна:
являются несовместными, то вероятность суммы этих событий равна:
а) 
б) 
в) 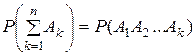
Дата добавления: 2014-12-23; просмотров: 392; Мы поможем в написании вашей работы!; Нарушение авторских прав |