
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи для самостоятельной работы. 4.1. Каждое из четырех несовместных событий может произойти соответственно с вероятностями 0,012, 0,010
4.1. Каждое из четырех несовместных событий может произойти соответственно с вероятностями 0,012, 0,010, 0,006 и 0,002. Определить вероятность того, что в результате опыта произойдет хотя бы одно из этих событий.
(Ответ: p = 0,03)
4.2. Стрелок производит один выстрел в мишень, состоящую из центрального круга и двух концентрических колец. Вероятности попадания в круг и кольца соответственно равны 0,20, 0,15 и 0,10. Определить вероятность непопадания в мишень.
(Ответ: p = 0,55)
4.3. Две одинаковые монеты радиуса r расположены внутри круга радиуса R, в который наудачу бросается точка. Определить вероятность того, что эта точка упадет на одну из монет, если монеты не перекрываются.
(Ответ: p =  )
)
4.4. Какова вероятность извлечь из колоды в 52 карты фигуру любой масти или карту пиковой масти (фигурой называется валет, дама или король)?
(Ответ: p =  )
)
4.5. В ящике имеются 10 монет по 20 коп., 5 монет по 15 коп. и 2 монеты по 10 коп. Наугад берутся шесть монет. Какова вероятность, что в сумме они составят не более одного рубля?
(Ответ: p =  )
)
4.6. В двух урнах находятся шары, отличающиеся только цветом, причем в первой урне 5 белых шаров, 11 черных и 8 красных, а во второй соответственно 10, 8 и 6. Из обеих урн наудачу извлекается по одному шару. Какова вероятность, что оба шара одного цвета?
(Ответ: p = 0,323)
4.7. Игра между A и B ведется на следующих условиях: в результате первого хода, который всегда делает А, он может выиграть с вероятностью 0,3; если первым ходом A не выигрывает, то ход делает В и может выиграть с вероятностью 0,5; если в результате этого хода В не выигрывает, то A делает второй ход, который может привести к его выигрышу с вероятностью 0,4. Определить вероятности выигрыша для А и для В.
(Ответ:  = 0,44,
= 0,44,  = 0,35)
= 0,35)
4.8. Вероятность для данного спортсмена улучшить свой предыдущий результат с одной попытки равна р. Определить вероятность того, что на соревнованиях спортсмен улучшит свой результат, если разрешается делать две попытки.
(Ответ: p(А) =  )
)
4.9. Из урны, содержащей n шаров с номерами от 1 до n, последовательно извлекаются два шара, причем первый шар возвращается, если его номер не равен единице. Определить вероятность того, что шар с номером 2 будет извлечен при втором извлечении.
(Ответ: p =  )
)
4.10. Игрок А поочередно играет с игроками В и С, имея вероятность выигрыша в каждой партии 0,25, и прекращает игру после первого проигрыша или после двух партий, сыгранных с каждым игроком. Определить вероятности выигрыша В и С.
(Ответ:  )
)
4.11. Двое поочередно бросают монету. Выигрывает тот, у которого раньше появится герб. Определить вероятности выигрыша для каждого из игроков.
(Ответ:  )
)
4.12. Вероятность получить очко, не теряя подачи, при игре двух равносильных волейбольных команд равна половине. Определить вероятность получения одного очка для подающей команды.
(Ответ:p = 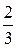 )
)
4.13. Два стрелка поочередно стреляют по мишени до первого попадания. Вероятность попадания для первого стрелка равна 0,2, а для второго равна 0,3. Найти вероятность того, что первый стрелок сделает больше выстрелов, чем второй.
(Ответ: p = 0,455)
4.14. Двое играют до победы, причем для этого необходимо первому выиграть т партий, а второму п партий. Вероятность выигрыша каждой партии первым игроком равна р, а вторым q=1—р. Определить вероятность выигрыша всей игры первым игроком.
(Ответ: p(A) = 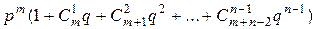 )
)
Дата добавления: 2014-12-23; просмотров: 760; Мы поможем в написании вашей работы!; Нарушение авторских прав |