
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение типовых задач. Пример 5.1. Среди n лиц разыгрываются т n выигрышей путем случайного извлечения из ящика n билетов
Пример 5.1. Среди n лиц разыгрываются т 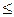 n выигрышей путем случайного извлечения из ящика n билетов. Одинаковы ли шансы выигрыша для любого из играющих? Когда выгоднее тащить билет?
n выигрышей путем случайного извлечения из ящика n билетов. Одинаковы ли шансы выигрыша для любого из играющих? Когда выгоднее тащить билет?
Решение.
Обозначим через Ak событие, состоящее в извлечении выигрышного билета после k извлечений билетов из ящика. По результатам предыдущих опытов можно сделать k+1 гипотез. Пусть гипотеза Hks означает, что из k извлеченных билетов выигрышных было s. Вероятности этих гипотез

причем
 .
.
Так как осталось n—k билетов, из которых т—s выигрышных, то при m 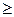 s
s
 .
.
По формуле полной вероятности находим
 ,
,
где  при s>m.
при s>m.
Данное равенство можно записать также в виде
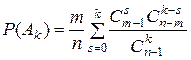 .
.
Имеем
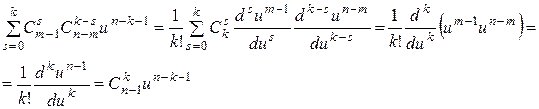 ,
,
т. е. справедливо равенство
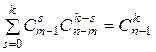 .
.
Искомая вероятность Р(Ak)= 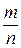 при любом k. Таким образом, у всех играющих шансы одинаковы и очередность извлечения не имеет значения.
при любом k. Таким образом, у всех играющих шансы одинаковы и очередность извлечения не имеет значения.
Пример 5.2. Отмеченный шар с вероятностями p и 1—p может находиться в первой или во второй урне. Вероятность извлечь отмеченный шар из урны, в которой этот шар находится, равна Р(Р 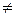 1). Как следует распорядиться правом n раз извлекать шары из любой урны, чтобы вероятность извлечения отмеченного шара хотя бы один раз была наибольшей, если шар после извлечения возвращается в урну?
1). Как следует распорядиться правом n раз извлекать шары из любой урны, чтобы вероятность извлечения отмеченного шара хотя бы один раз была наибольшей, если шар после извлечения возвращается в урну?
Решение.
Пусть событие А — извлечение отмеченного шара.
Гипотезы: H1—шар находится в первой урне, H2—во второй.
По условию P(H1)=p, Р(H2)=1—р.
Допустим, что из первой урны извлечено т, а из второй n—т шаров. Условные вероятности извлечения отмеченного шара будут
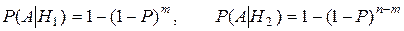 .
.
По формуле полной вероятности искомая вероятность
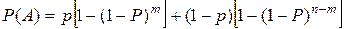 .
.
Нужно определить т так, чтобы была наибольшей вероятность Р (А). Дифференцируя Р(A) по т (для нахождения приближенного значения т считаем m непрерывным), получаем
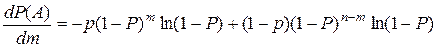 .
.
Полагая, 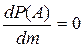 приходим к равенству
приходим к равенству
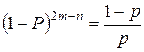 .
.
Поэтому должно быть
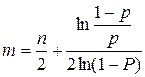 .
.
Дата добавления: 2014-12-23; просмотров: 462; Мы поможем в написании вашей работы!; Нарушение авторских прав |