Краткая теоретическая часть. Получим важные формулы Бейеса или, как иногда говорят, формулы вероятности гипотез

Получим важные формулы Бейеса или, как иногда говорят, формулы вероятности гипотез. Требуется найти вероятность события A_i , если известно, что В произошло. Согласно теореме умножения имеем:

(6.1)

Из соотношения (6.1) получаем

(6.2)

Используя формулу полной вероятности (5.1), находим:

(6.3)

Полученные формулы (6.3) носят название формул Бейеса. Общая схема применения этих формул к решению практических задач такова. Пусть событие В может протекать в различных условиях, относительно характера которых может быть сделано n гипотез: . По тем или иным причинам нам известны вероятности этих гипотез до испытания (априорные вероятности гипотез). Известно также, что гипотеза сообщает событию вероятность 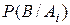. Произведен опыт, в котором событие В наступило. Это должно вызвать переоценку вероятностей гипотез ; формулы Бейеса количественно решают этот вопрос.

Вероятности называются апостериорными вероятностямисобытия .

Тест

1. При решении каких задач следует применить формулу Бейеса?

а) Найти вероятность события В, которое зависит от гипотез

б) Найти вероятность справедливости гипотезы при условии, что связанное с ней событие В произошло

в) Найти апостериорную вероятность гипотезы при условии, что событие В, связанное с ней, имело место

г) Найти априорную вероятность гипотезы при условии, что событие В, связанное с ней, имело место

д) Найти вероятность справедливости гипотезы в проводимом опыте

2. Какие условия должны накладываться на событие В и гипотезы ?

а) Гипотезы представляют собой полную группу несовместных событий

б) Гипотезы представляют собой полную группу равновозможных событий

в) Событие В может протекать в различных условиях, относительно характера которых может быть сделано n гипотез

г) Событие В может протекать в различных условиях, относительно характера которых не может быть сделана ни одна из n гипотез

3. Какой вид имеет формула Бейеса?

а)

б)

в)

4. Как называются вероятности ?

а) Априорные вероятности события

б) Апостериорные вероятности события