Краткая теоретическая часть

В настоящем разделе мы изучим основные закономерности, относя­щиеся к одной из важнейших схем теории вероятностей — схеме по­следовательных независимых испытаний. В это понятие мы вклады­ваем следующий смысл.

Под испытанием(опытом) мы станем понимать осуществление опреде­ленного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства U элементарных событий. Математической моделью последовательности п испытаний является новое пространство элементарных событий, состоящее из точек , где - произвольная точка пространства U, отвечающая испытанию с номером i.

Предположим, что для s-го испытания пространство U разбито на k несовместимых случайных событий , т. е. предположим, что

Событие назовем i-м исходом при s-м испытании. Обозначим вероятность i-го исхода при s-м испытании через .

Обозначим через событие, состоящее из всех тех точек пространства , для которых . Если в пространстве U_n имеет место равенство при любых - то испытания называются независимыми.

В дальнейшем мы ограничимся случаем, когда вероятности собы­тий не зависят от номера испытания s; обозначим в этом случае 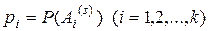; в силу несовместимости и единственной возможности исходов очевидно, имеем . Эта схема впервые была рассмотрена Я. Бернулли в важнейшем частном случае ; по этой причине указанный случай носит название схемы Бернулли. В схеме Бернулли обычно полагают .

Из определения независимых испытаний вытекает следующий результат:

Теорема. Если данные п испытаний независимы, то любые т из них также независимы.

Простейшая задача, относящаяся к схеме независимых испытаний, состоит в определении вероятности того, что при п испыта­ниях событие А наступит т раз, а остальные п—т раз наступит противоположное событие , обозначим это событие В. Тогда

(7.1)

Здесь А_i – событие состоящее в том, что событие А произойдет в i- ом испытании. Событие В представляет собой сумму несовместных событий, тогда согласно теореме сложения вероятностей получаем

(7.2)

Вероятность каждого слагаемого в данной сумме по теореме умножения для независимых событий равна . По теореме сложения вероятностей искомая вероятность равна сумме только что вычисленных вероятностей для всех различных способов т появлений события А и n—т не появлений среди п испы­таний. Число таких способов, как известно из теории сочетаний, равно ; следовательно, искомая вероятность равна

(7.3)

Так как все возможные несовместимые между собой исходы п испытаний состоят в появлении события 0 раз, 1 раз, 2 раза, ..., n раз, то ясно, что

(7.4)

Легко заметить, что вероятность равна коэффициенту при в разложении бинома по степеням x.

Исследуем далее, как ведет себя вероятность при различных значениях m. 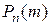с увеличением m сначала возрастает, затем достигает максимума и при дальнейшем росте m убывает. При этом, если 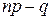является целым числом, то максимальное значение вероятность принимает для двух значений m, а именно и . Если же 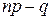не является целым числом, то максимальное значение вероятности достигается при , равном максимальному целому числу, большему из и . Число называют наивероятнейшим значением и обозначают через .

Поставим теперь более общую задачу.

Рассмотрим последовательность n независимых испытаний, в каждом из которых может произойти или не произойти некоторое событие А. При этом вероятность появления события в каждом испытании различна.

Обозначим через . А_i – событие состоящее том что А произойдет в i-ом испытании – событие состоящее том что А не произойдет в i-ом испытании соответственно.

Следует определить вероятность того что событие А произойдет m раз в серии из n испытаний.

Вероятность того, что событие А произойдет m раз в серии из n испытаний равна коэффициенту при в выражении производящей функции

(7.5)

то есть

	(7.6)
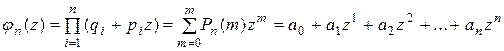
	(7.7)

Обозначим через событие состоящее в том, что А появляется не менее m раз в n независимых испытаниях, а вероятность обозначим , тогда

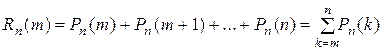
(7.8)

В тех случаях когда удобно пользоваться следующей формулой

(7.9)

Тест

Вычисление вероятностей появления события при повторных независимых испытаниях.

1. В каком случае опыты называют независимыми?

а) Если вероятности исходов (событий) в каждом из предыдущих опытов не влияют на вероятности этих исходов в последующих опытах

б) Если вероятности исходов в каждом из опытов не зависят от порядка следования этих опытов

в) Вероятности исходов (событий) в каждом из предыдущих опытов влияют на вероятности этих исходов в последующих опытах

2. Если вероятность появления события в каждом из опытов одинакова, то вероятность появления события m раз при n опытах с ростом m меняется следующим образом:

а) Сначала убывает, затем достигает своего наименьшего значения, а потом увеличивается

б) Монотонно убывает

в) Сохраняет постоянное значение

г) Монотонно возрастает

д)Сначала возрастает, затем достигает своего наибольшего значения, а потом уменьшается

3. Если вероятность появления события в каждом из опытов одинакова, то вероятность появления события А m раз при n опытах определяется по формуле

а)

б)

в)

г)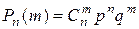

4. Укажите формулы, по которой можно вычислить вероятность появления события А не менее m раз при n опытах , если вероятность появления события А в каждом из опытов одинакова

а)

б)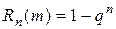

в)

5. Чему равно наивероятнейшее значение числа m появлений события, если вероятность появления события в каждом из опытов одинакова?

а) Целой части числа

б) Максимальному целому числу, большему из и

в) Целой части числа , если оно является дробным, или максимальному целому числу, большему из и , если является целым

6. Если опыты независимы, но вероятности появления события А в каждом из них различны, то вероятность появления события m раз при n опытах равна коэффициенту при в разложении производящей функции, которая имеет вид:

а)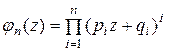

б)

в)