А) Ряд, многоугольник и функция распределения случайной дискретной величины

Пример 8.1. Из партии, содержащей 100 изделий, среди которых имеется 10 дефектных, выбраны случайным образом пять изделий для проверки их качества. Построить ряд распределений случайного числа Х дефектных изделий, содержащихся в выборке.

Решение.

Введем в рассмотрение случайную величину X – число дефектных изделий среди выбранных пяти. Так как в выборке число дефектных изделий может быть любым целым числом в пределах от 0 до 5 включительно, то возможные значения x_i, случайной величины Х равны:

x₁ = 0, x₂ = 1, x₃ = 2, x₄ = 3, x₅ = 4, x₆ = 5.

Вероятность Р(X = k) того, что в выборке окажется ровно k (k=0, 1, 2, 3, 4, 5) дефектных изделий, равна

.

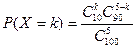В результате расчетов по данной формуле с точностью до 0,001 получим:

p₁ = P(X = 0)=0,583, p₁ = P(X = 1)=0,340,

p₁ = P(X = 2)=0,070, p₁ = P(X = 3)=0,007,

p₁ = P(X = 4)=0, p₁ = P(X = 5)=0.

Используя для проверки равенство , убеждаемся, что расчеты и округление произведены правильно (см. табл. 2).

Таблица 2

Пример 8.2. Изделия испытываются при перегру­зочных режимах. Вероятности для каждого изделия пройти испытание равны 4/5 и независимы. Испытания заканчиваются после первого же изделия, не выдержавшего испытания. Вывести формулу для ряда распределения числа испытаний.

Решение.

Введем в рассмотрение случайную величину X – число взятых изделий для испытаний. Испытания заканчиваются на k-м изделии (k = 1, 2, 3, ...), если первые k—1 изделий пройдут испытания, a k - e изделие не выдержит испытания.

Если Х — случайное число испытаний, то

Полученная формула для ряда распределения эквивалентна таблице 3.

Таблица 3.

xi				…	k	…
pi				…		…

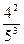
Особенность данной задачи состоит в том, что теоретически число испытаний может быть бесконечно большим, однако вероятность такого события стремится к нулю:

Пример 8.3. На пути движения автомашины четыре светофора. Каждый из них с вероятностью 0,5 либо разре­шает, либо запрещает автомашине дальнейшее движение.

Решение.

Х — случайное число светофоров, пройден­ных автомашиной без остановки; оно может принимать сле­дующие значения:

x₁ = 0, x₂ = 1, x₃ = 2, x₄ = 3, x₅ = 4,

Вероятности p_i = P(X=x_i) того, что число пройденных светофоров Х будет равно данному частному значению, вычисляются по формуле

где p — вероятность для светофора задержать автомашину (p = 0,5).

В результате вычислений получим

p₁ = 0,5, p₂ = 0,25, p₃ = 0,125, p₄ = 0,0625,p₅ = 0,0б25.

По полученным данным строим многоугольник распределения вероятностей (рис. 2).

Пример 8.4. Космическая ракета имеет прибор, состоящий из четырех блоков a₁, a₂, a₃ и a₄, каждый из которых дает отказ при попадании в него хотя бы одной элементарной частицы. Отказ прибора в целом наступает как при отказе блока a₁, так и при одновременном отказе всех трех блоков a₂, a₃ и a₄.

Построить функцию распределения F(x) случайного числа Х частиц, после попадания которых в прибор он дает отказ, если вероятность частице, попавшей в прибор, попасть в блок a₁ равна p₁ = 0,4, а в блоки a₂, a₃ и a₄ соответственно равна p₂ = p₃ = p₄ = 0,2.

Решение.

Обозначим A₁, A₂, A₃ и A₄ события, состоящие в отказе блоков a₁, a₂, a₃ и a₄ соответственно. Искомая функция распределения F(x) равна вероятности того, что при числе попаданий n<x прибор выйдет из строя, т. е.

F(x) = P(A₁+A₂A₃A₄)

Используя формулу

и применяя формулу сложения вероятностей, получим

где все вероятности определяются при условии попадания в прибор n(n>1) частиц. Так кaк

p₁ + p₂ + p₃ + p₄ = 1

и при каждом попадании частицы в прибор обязательно дает отказ один и только один из блоков, то

Таким образом, учитывая, что p₂ = p₃ = p₄ = 0,2, получим

,

где под [x] понимается наибольшее целое число, меньшее x, например [5,9] = 5, [5] = 4. При n 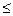1 F(x) = 0.

Таким образом, график функции распределения вероятностей для нескольких начальных значений x имеет вид, представленный на рис. 3.