А) Ряд, многоугольник и функция распределения случайной дискретной величины. Случайная величина называется дискретной, если ее частные (возможные) значения можно пронумеровать.

Случайная величина называется дискретной, если ее частные (возможные) значения можно пронумеровать.

Дискретная случайная величина Х может быть задана рядом распределения или функцией распределения (инте­гральным законом распределения).

Рядом распределения называется совокупность всех воз­можных значений x_i, и соответствующих им вероятностей p_i = P(X = x_i). Ряд распределения может быть задан в виде таблицы (табл. 1) или формулой.

Таблица 1.

Вероятности p_i удовлетворяют условию

,

где число возможных значений n может быть конечным или бесконечным.

Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения случайной величины (x_i) откладываются по оси абсцисс, а вероятности p_i - по оси ординат; точки A_i с координатами (x_i ; p_i) соединяются ломаными линиями (рис. 1).

Функцией распределения (интегральным законом распределения) случайной величины Х называется функция F (x), равная вероятности P(X<x) того, что случайная величина будет меньше произвольно выбранного значения x. Функция F(x) вычисляется по формуле

,

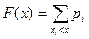где суммирование ведется по всем значениям i, для которых x_i<x.

б) Функция распределения и плотность вероятности непрерывной случайной величины

Случайная величина называется непрерывной, если существует неотрицательная функция f(x), удовлетворяющая при любых x равенству

.

Функция f(x) называется плотностью вероятности

.

Непрерывная случайная величина задается либо функцией распределения F(x) (интегральным законом распределения), либо плотностью вероятности f(x) (дифференциальным законом распределения).

Функция распределения F(x) = Р(X<x), где x — произвольное действительное число, дает вероятность того, что случайная величина Х окажется меньше x.

Функция распределения F(x) имеет следующие основные свойства:

Плотность вероятности (дифференциальный закон распределения) f(x) обладает следующими основными свойствами:

Величина x_p, определяемая равенством F(x_p) = p, называется квантилем порядка p, квантиль x_0,5 называют медианой. Если плотность имеет максимум, то значение x, при котором f(x) достигает максимума, называется модой.

Тест

Дискретные и непрерывные случайные величины.

1. Какое из данных утверждений не является определением случайной величины?

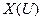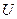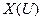а) Случайной величиной называется вещественная функция, определенная на элементах пространства элементарных исходов таким образом, что для любого числа , принадлежащего вещественной прямой, множество , на котором функция удовлетворяет неравенству , является элементом поля событий , то есть

б) Функция 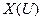называется случайной величиной, если для любого события ( ) определена его вероятность

в) является случайной величиной, если для него определена вероятность

г) Функция 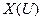есть случайная величина, если для любого , принадлежащего вещественной прямой, событие достоверно, то есть

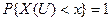
2. Какое из следующих утверждений является определением функции распределения случайной величины?

а) Вероятность является некоторой функцией аргумента и называется функцией распределения случайной величины X

б) Вероятность является постоянной величиной и называется функцией распределения случайной величины X

в) Вероятность является некоторой функцией аргумента 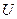и называется функцией распределения случайной величины X

3. Знание функции распределения случайной величины полностью с вероятностной точки зрения характеризует случайную величину. А что она определяет?

а) Функция распределения случайной величины определяет вероятность того, что случайная величина окажется меньше числа , где - произвольное действительное число

б) Функция распределения случайной величины определяет вероятность того, что случайная величина окажется больше числа , где - произвольное действительное число

в) Функция распределения случайной величины определяет вероятность того, что случайная величина окажется равной числу , где - произвольное действительное число

4. Плотность распределения – это понятие, применимое:

Дата добавления: 2014-12-23; просмотров: 36; Нарушение авторских прав