Задачи для самостоятельной работы. 6.1. Имеется десять одинаковых урн, из которых в девяти находятся по два черных и по два белых шара

6.1. Имеется десять одинаковых урн, из которых в девяти находятся по два черных и по два белых шара, а в одной— пять белых и один черный шар. Из урны, взятой наудачу, извлечен белый шар. Какова вероятность, что шар извлечен из урны, содержащей пять белых шаров?

(Ответ: p = )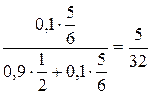

6.2. Известно, что 96°/о выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,98 и нестандартную — с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.

(Ответ: p = 0,998)

6.3. Из партии в пять изделий наудачу взято одно изделие, оказавшееся бракованным. Количество бракованных изделий равновозможно любое. Какое предположение о количестве бракованных изделий наиболее вероятно?

(Ответ: Пять бракованных изделий )

6.4. Игрок D играет с неизвестным противником на следующих условиях: ничейный исход исключен; первый ход делает противник; в случае его проигрыша делает ход D, выигрыш которого означает выигрыш игры, а при проигрыше игра повторяется второй раз на тех же условиях. Из двух равновозможных противников В имеет вероятность выиграть первым ходом 0,4, а вторым — 0,3; С имеет вероятность выиграть первым ходом 0,8, а вторым ходом 0,6. Для D вероятность выиграть первым ходом равна 0,3 и не зависит от противника, а для второго хода равна 0,5 при игре с В и 0,7 при игре с C. Игру выиграл D.

Какова вероятность:

а) что противником был В;

б) что противником был С?

(Ответ: а) p =0,59; б) p = 0,41)

6.5. Из 18 стрелков 5 попадают в мишень с вероятностью 0,8; 7 — с вероятностью 0,7; 4 — с вероятностью 0,6 и 2 — с вероятностью 0,5. Наудачу выбранный стрелок произвел выстрел, но в мишень не попал. К какой из групп вероятнее всего принадлежал этот стрелок?

(Ответ: Ко второй группе)

6.6. Вероятности попадания при каждом выстреле для трех стрелков равны соответственно . При одновременном выстреле всех трех стрелков имелось два попадания. Определить вероятность того, что промахнулся третий стрелок.

(Ответ: p = )

6.7. Трое охотников одновременно выстрелили по вепрю, который был убит одной пулей. Определить вероятности того, что вепрь убит первым, вторым или третьим охотником, если вероятности попадания для них равны соответственно 0,2; 0,4; 0,6.

(Ответ: = 0,103; = 0,277; 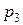= 0,620)

6.8. Два стрелка поочередно стреляют в мишень. Вероятности попадания первыми выстрелами для них равны соответственно 0,4 и 0,5, а вероятности попадания при последующих выстрелах для каждого увеличиваются на 0,05. Какова вероятность, что первым произвел выстрел первый стрелок, если при пятом выстреле произошло попадание в мишень?

(Ответ: p = )

6.9. Произведено три независимых испытания, в каждом из которых событие A происходит с вероятностью 0,2. Вероятность появления другого события В зависит от числа появлений события A: при однократном появлении события A эта вероятность равна 0,1, при двукратном появлении равна 0,3, при трехкратном появлении равна 0,7; если событие A не имело места ни разу, то событие В невозможно. Определить наивероятнейшее число появлений события A, если событие В имело место.

(Ответ: Одно появление)

6.10. Получена партия из восьми изделий одного образца. По данным проверки половины партии, три изделия оказались технически исправными, а одно бракованным. Какова вероятность, что при проверке трех последующих изделий одно из них окажется исправным, а два бракованными, если любое количество бракованных изделий в данной партии равновозможно?

(Ответ: p = ).