Занятие 5. Формула полной вероятности.

Краткая теоретическая часть

Предположим, что событие В может осуществиться с одним и только с одним из n несовместимых событий . Иными словами, положим , где события BA_i и BA_j с разными индексами i и j несовместимы. По теореме сложения вероятностей имеем: .

Применяя теорему умножения, находим:

(5.1)

Это равенство носит название формулы полной вероятности и играет важную роль во всей дальнейшей теории.

Тест.

1. Пусть - некоторые события. Укажите 2 условия, при которых необходимо применить формулу полной вероятности для определения вероятности появления события :

а) - полная группа несовместных событий

б) - полная группа равновозможных событий

в) - полная группа независимых событий

г) - полная группа попарно несовместных и равновозможных событий

д) Событие не может произойти совместно ни с одним из событий

е) Событие может произойти совместно только с одним из событий

ж) Событие может произойти совместно с каждым из событий

2. Что означает тот факт, что - полная группа несовместных событий?

а)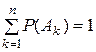

б)

в)

3. Какие из следующих групп событий , не являются полными группами несовместных событий?

а) - извлечение шара из -той урны, содержащей белых и черных шаров, если шар извлекается наудачу из любой из урн

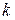б) - извлечение шара из -той урны, содержащей белых и черных шаров, если шар извлекается наудачу из любых двух урн

в) - наличие 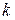бракованных лампочек среди 100 взятых наудачу из 1000, если известно, что число испорченных лампочек на 1000 штук равновозможно от 0 до 5

г) - правильный ответ студента по крайней мере на 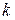из вопросов, содержащихся в экзаменационных билетах

д) - правильный ответ студента ровно на 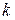из вопросов, содержащихся в экзаменационных билетах

4. Какой вид имеет формула полной вероятности?

а)

б)

в)

г)

Дата добавления: 2014-12-23; просмотров: 17; Нарушение авторских прав