Решение типовых задач. Пример 7.1. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен):

Пример 7.1. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен):

а) три партии из четырех или пять из восьми;

б) не менее трех партий из четырех или не менее пяти партий из восьми?

Решение.

Так как противники равносильные, то вероятности выигрыша и проигрыша каждой партии одинаковы и равны p = q = l/2.

а) Вероятность выиграть три партии из четырех

Вероятность выиграть пять партий из восьми

.

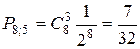Так как , то вероятнее выиграть три партии из четырех.

б) Вероятность выиграть не менее трех партий из четырех

,

а вероятность выиграть не менее пяти партий из восьми

.

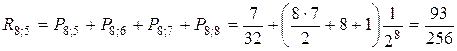Так как , то вероятнее выиграть не менее пяти партий из восьми.

Пример 7.2. Имеется шесть потребителей электрического тока, для первого из которых при определенных условиях вероятность того, что произойдет авария, приводящая к отклю­чению потребителя, равна 0,6, для второго — 0,2, а для четырех остальных — по 0,3. Определить вероятность того, что генератор тока будет отключен полностью:

а) если все потребители соединены последовательно;

б) если потребители соединены так, как показано на схеме (рис. 6).

Решение.

а) Вероятность неотключения всех шести потребителей равна произведению вероятностей неотключения каждого потребителя, т. е.

.

Искомая вероятность равна вероятности отключения хотя бы одного потребителя, т. е. .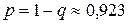

б) В этом случае генератор будет отключен полностью, если в каждой паре последовательно соединенных потребителей отключен хотя бы один потребитель:

.

Пример 7.3. Большая партия изделий содержит один процент брака. Каков должен быть объем случайной выборки, чтобы вероятность встретить в ней хотя бы одно бракованное изделие была не меньше 0,95?

Решение.

Искомое число n находится по формуле .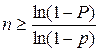

В данном случае 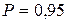, а 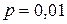. Поэтому .

Пример 7.4. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0,4 независимо от заявок других магазинов. Найти наивероятнейшее число заявок в день и вероятность получения этого числа заявок.

Решение.

В данном случае n = 10, p = 0,4, (n + 1)p = 4,4. Наивероятнейшеё число , заявок равно целой части числа (n + 1)p, т. е. p = 4.

Вероятность четырёх заявок из десяти

.