
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение типовых задач. Пример 9.1. Партия, насчитывающая 100 изделий, содержит 10 дефектных
Пример 9.1. Партия, насчитывающая 100 изделий, содержит 10 дефектных. Из всей партии случайным образом отбираются с целью проверки качества 5 изделий (случайная выборка). Найти математическое ожидание числа дефектных изделий, содержащихся в случайной выборке.
Решение.
Случайное число дефектных изделий, содержащихся в выборке, может иметь следующие значения:

Вероятности  того, что X принимает данное значение
того, что X принимает данное значение  , равны (см. пример 8.1)
, равны (см. пример 8.1)
 (
(  1, 2, 3, 4, 5, 6).
1, 2, 3, 4, 5, 6).
Искомое математическое ожидание
 .
.
Так как  есть коэффициент при
есть коэффициент при  в произведении
в произведении  , то
, то  есть коэффициент при
есть коэффициент при  в выражении
в выражении
 .
.
Следовательно,
 , а
, а 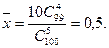
Пример 9.2. Дискретная случайная величина  задана рядом распределения
задана рядом распределения  1, 2, 3, … ,
1, 2, 3, … ,  .Выразить математическое ожидание случайной величины
.Выразить математическое ожидание случайной величины  через производящую функцию
через производящую функцию
 .
.
Решение.
По определению математического ожидания случайной величины
 .
.
С другой стороны, значение производной от производящей функции, вычисленное при  , равно
, равно
 .
.
Следовательно,
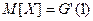 .
.
Пример 9.3. Опыт может быть успешным с вероятностью р и неуспешным с вероятностью 1 —р.
Условная вероятность достижения намеченного результата после т успешных опытов Р(т) равна
 .
.
Найти математическое ожидание числа независимых опытов, необходимых для достижения намеченного результата.
Решение.
Обозначим  вероятность достижения намеченного результата при
вероятность достижения намеченного результата при  опытах. Если
опытах. Если  — вероятность иметь ровно т успешных из общего числа п опытов, то согласно формуле полной вероятности
— вероятность иметь ровно т успешных из общего числа п опытов, то согласно формуле полной вероятности

Так как опыты независимы и вероятность успешного исхода в каждом из них равна р, то
 .
.
Подставляя в формулу для  значения
значения  и Р(т), получим
и Р(т), получим
 .
.
Для достижения намеченного результата потребуется ровно п опытов, если при п-м опыте он будет достигнут. Вероятность последнего события равна  . Следовательно, математическое ожидание случайного числа опытов, необходимых для достижения намеченного результата,
. Следовательно, математическое ожидание случайного числа опытов, необходимых для достижения намеченного результата,

Для вычисления последней суммы воспользуемся равенством
 ,
,
справедливым при  . Полагая в данном случае
. Полагая в данном случае  , получим
, получим
 .
.
Пример 9.4. Прибор имеет п предохранителей. В случае перегрузки сгорает один из предохранителей, который заменяется новым. Каково математическое ожидание  числа перегрузок
числа перегрузок  , после которых в приборе окажутся замененными все первоначально установленные предохранители, если выход из строя в момент перегрузки любого из п предохранителей (как незамененного, так и нового) равновероятен?
, после которых в приборе окажутся замененными все первоначально установленные предохранители, если выход из строя в момент перегрузки любого из п предохранителей (как незамененного, так и нового) равновероятен?
Решение.
Обозначим  математическое ожидание числа перегрузок, после которых все первоначально установленные п предохранителей окажутся замененными, если остались незамененными
математическое ожидание числа перегрузок, после которых все первоначально установленные п предохранителей окажутся замененными, если остались незамененными  предохранителей.
предохранителей.
Для вычисления  воспользуемся формулой полного математического ожидания. Если остались незамененными
воспользуемся формулой полного математического ожидания. Если остались незамененными  предохранителей
предохранителей  , то для повреждения одного из них потребуется очередная перегрузка. В зависимости от результатов очередной перегрузки будут различными средние числа перегрузок, необходимых для сгорания предохранителей, оставшихся из числа первоначально установленных.
, то для повреждения одного из них потребуется очередная перегрузка. В зависимости от результатов очередной перегрузки будут различными средние числа перегрузок, необходимых для сгорания предохранителей, оставшихся из числа первоначально установленных.
При очередной перегрузке могут произойти два события:
 — сгорел один из первоначально установленных предохранителей, вероятность чего
— сгорел один из первоначально установленных предохранителей, вероятность чего  ;
;
 — сгорел замененный предохранитель, вероятность чего
— сгорел замененный предохранитель, вероятность чего 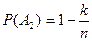 .
.
Если при очередной перегрузке произойдет событие  , то математическое ожидание числа перегрузок для замены всех
, то математическое ожидание числа перегрузок для замены всех  предохранителей, не замененных до очередной перегрузки, будет равно
предохранителей, не замененных до очередной перегрузки, будет равно 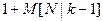 . Если же при очередной перегрузке произойдет событие А2, то это математическое ожидание будет равно
. Если же при очередной перегрузке произойдет событие А2, то это математическое ожидание будет равно  . На основании формулы полного математического ожидания имеем
. На основании формулы полного математического ожидания имеем

или, после несложных преобразований,
 .
.
Если  , т. е. остался лишь один незамененный.предохранитель, то вероятность его замены равна
, т. е. остался лишь один незамененный.предохранитель, то вероятность его замены равна  . Следовательно, на основании примера 9.3 будем иметь
. Следовательно, на основании примера 9.3 будем иметь

Итак, имеем цепь равенств:

суммируя которые, получим

или
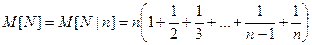 .
.
Пример 9.5. В результате испытаний двух приборов (А и В) установлена вероятность появления помех, оцениваемых по трехбалльной системе (табл. 6). (В случае отсутствия помех их уровень принимается равным нулю).
Таблица 6.
| Уровень помех | ||||
| Вероятность появления помех данного уровня | Прибор А | 0,20 | 0,06 | 0,04 |
| Прибор В | 0,06 | 0,04 | 0,10 |
По приведенным данным выбрать лучший прибор, если лучшим является тот, который в среднем имеет меньший уровень помех.
Решение.
Обозначим через X случайный уровень помех. Средний уровень помех для прибора А
 балла.
балла.
Для прибора В
 балла.
балла.
Итак, по среднему баллу оба прибора равноценны. В качестве дополнительного критерия сравнения используем среднее квадратическое отклонение уровня помех:
 балла,
балла,
 балла.
балла.
Таким образом, прибор А дает более устойчивые показания относительно средних, и, следовательно, он лучше прибора В.
Дата добавления: 2014-12-23; просмотров: 1495; Мы поможем в написании вашей работы!; Нарушение авторских прав |