
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение типовых задач. Пример 10.1. Плотность вероятности случайных амплитуд боковой качки корабля имеет вид (закон Рэлея)
Пример 10.1. Плотность вероятности случайных амплитуд боковой качки корабля имеет вид (закон Рэлея)
 .
.
Определить:
а) математическое ожидание М[X];
б) дисперсию D[Х] и среднее квадратическое отклонение 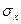 ;
;
в) центральные моменты третьего и четвертого порядков  и
и 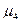 .
.
Решение.
Вычисление моментов сводится к вычислению интегралов вида
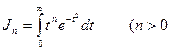 целое),
целое),
которые равны: при n четном
 ,
,
где
 ,
,
и при n нечетном

 .
.
Математическое ожидание случайной амплитуды боковой качки равно
 .
.
Произведя замену переменных  , получим
, получим
 .
.
б) Так как
 , то
, то
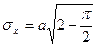 .
.
в)  ,
,
где  .
.
Следовательно,
 ,
,
 , где
, где 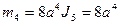
Следовательно,  .
.
Пример 10.2. Найти срединное отклонение случайной величины, плотность вероятности которой имеет вид (распределение Лапласа)
 .
.
Решение.
Так как плотность вероятности симметрична относительно нуля, то  . Срединное отклонение Е вычисляется по формуле
. Срединное отклонение Е вычисляется по формуле
 .
.
Отсюда 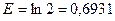 .
.
Дата добавления: 2014-12-23; просмотров: 509; Мы поможем в написании вашей работы!; Нарушение авторских прав |