Решение типовых задач

Пример 11.1. Радиоаппаратура состоит из 1000 электроэлементов. Вероятность отказа одного элемента в течение одного года работы равна 0,001 и не зависит от состояния других элементов. Какова вероятность отказа двух и не менее двух электроэлементов за год?

Решение.

Считая случайное число X отказавших элементов подчиняющимся закону Пуассона

, где , получим:

1) вероятность отказа ровно двух элементов

;

2) вероятность отказа не менее двух элементов

.

Пример 11.2. При разрыве баллона в процессе испытания на прочность образовалось 100 осколков, распределившихся равномерно в «конусе разлета», т. е. в области, ограниченной двумя коническими поверхностями с углами 30° и 60° (см. рис.). Найти математическое ожидание и дисперсию числа осколков, приходящихся на 1 м² части поверхности сферы, находящейся внутри конуса разлета, если радиус сферы 50 м, а центр ее совпадает с точкой разрыва.

Решение.

Пересечем конус разлета осколков сферой радиуса 50 м и определим математическое ожидание числа осколков, приходящихся на единицу площади поверхности шарового пояса, образовавшегося в результате пересечения конуса разлета со сферой. Обозначим через S площадь поверхности шарового пояса:

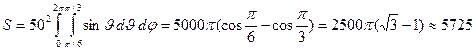м²

Так как общее число осколков N=100, то математическое ожидание числа их а, приходящегося на единицу площади поверхности шарового пояса, будет

осколка.

Вероятность попадания данного осколка в данную площадку м² мала (она равна , а направления полета осколков взаимно независимы; поэтому можно считать, что случайное число осколков X, приходящееся на 1 м² поверхности сферы, распределено по закону Пуассона и, следовательно, имеет место равенство

.