Занятие 12. Закон нормального распределения.

Краткая теоретическая часть

Плотность вероятности нормально распределенной случайной величины имеет вид

или

,

где - среднее квадратическое отклонение, - срединное отклонение (иногда называемое и «вероятным отклонением»),

Вероятность попадания нормально распределенной случайной величины X в интервал вычисляется по одной из следующих формул:

1) ,

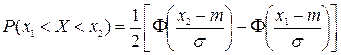где - функция Лапласа (интеграл вероятности);

2) ,

где - приведенная функция Лапласа.

Значения функци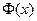й и даны в специальных таблицах.

Во всех задачах данного параграфа ошибки измерения считаются нормальными величинами.

Тест

1. Нормальное распределение играет достаточно важную роль в теории вероятностей и среди законов занимает особое положение. Укажите причины, по которым, на Ваш взгляд, это происходит:

а) Это наиболее часто употребляемый во многих приложениях закон распределения

б) Нормальный закон распределения применим как для дискретных, так и для непрерывных случайных величин

в) Нормальный закон распределения является предельным законом, к которому сходятся другие при весьма типичных часто встречающихся условиях

г) Нормальный закон распределения таков, что позволяет характеризовать сравнительную крутость других законов относительно него

2. Плотность вероятности нормально распределенной случайной величины имеет вид:

а)

б)

в) или

г)

д)

е) или

3. Параметры и 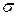закона нормального распределения совпадают с математическим ожиданием и среднеквадратическим отклонением нормально распределенной случайной величины соответственно. Следовательно, они определенным образом характеризуют случайную величину. А как? Выберите наиболее точный, на Ваш взгляд, вариант ответа.

а) Характеризуют форму кривой распределения и положение распределения случайной величины на оси абсцисс соответственно

б) Характеризуют положение распределения случайной величины на оси абсцисс и форму кривой распределения соответственно

в) Определяют центр рассеянья и центр симметрии случайной величины соответственно

г) Определяют центр симметрии и центр рассеянья случайной величины соответственно

4. Какой особенностью обладают моменты нормального распределения?

а) Все четные центральные моменты равны нулю.

б) Все нечетные центральные моменты равны нулю.

в) Все центральные моменты равны нулю

5. Одной из формул, по которым можно вычислить вероятность попадания нормально распределенной случайной величины в заданный интервал является (здесь - функция Лапласа (интеграл вероятности)):

а)

б)

в)

г)

6. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, обладают следующим свойством:

а) равны нулю

б) равны между собой

в) равны параметру Пуассона