КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи для самостоятельной работы. 10.1. Плотность вероятности случайной величины Х имеет вид (закон равномерного распределения)
10.1. Плотность вероятности случайной величины Х имеет вид (закон равномерного распределения)
Определить:
а) 
;
б) 
;
в) найти связь между средним квадратическим и срединным отклонениями случайной величины Х.
(Ответ: а) 
; б) 
в) 
)
10.2. Функция распределения случайной величины Х имеет вид (закон арксинуса)
Определить постоянные a и b. Найти и .
(Ответ: 
)
10.3. Определить математическое ожидание и дисперсию случайной величины Х, если плотность вероятности
(Ответ: 
)
10.4. Плотность вероятности случайной величины Х имеет вид (закон арксинуса)
.
Определить дисперсию и срединное отклонение.
(Ответ: 
)
10.5. Плотность вероятности случайных амплитуд А боковой качки корабля определяется формулой (закон Рэлея)
,
где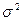 
- дисперсия угла крена.
Одинаково ли часто встречаются амплитуды, меньшие и большие средней?
(Ответ: 
; 
)
10.6. Скорость молекул газа имеет плотность вероятности (закон Максвелла)
.
Найти математическое ожидание и дисперсию скорости молекул, а также величину А при заданном h.
(Ответ: 
)
10.7. Плотность вероятности случайной величины X задана в виде
Определить и .
(Ответ: 
)
10.8. Функция распределения случайной величины X имеет вид
Найти М[Х] и D[X].
(Ответ: 
)
10.9. Найти математическое ожидание и дисперсию случайной величины, плотность вероятности которой имеет вид (распределение Лапласа):
.
(Ответ: 
)
10.10. Случайная величина X имеет плотность вероятности (гамма-распределение)
Определить параметр А, математическое ожидание и дисперсию случайной величины X.
(Ответ: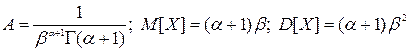 
)
10.11. Случайная величина X имеет плотность вероятности (бета-распределение)
Определить параметр А, математическое ожидание и дисперсию случайной величины X.
(Ответ: 
)
10.12. Случайная величина X имеет плотность вероятности
,
где 
— целое положительное число, большее 1. Определить постоянную А, математическое ожидание и дисперсию случайной величины X.
(Ответ: 
Указание: Для вычисления интеграла 
следует воспользоваться подстановкой 
, приводящей к бета-функции, а последнюю выразить через гамма-функцию)
10.13. Плотность вероятности неотрицательной случайной величины X имеет вид ( 
-распределение)
,
где 
.
Определить А, математическое ожидание и дисперсию случайной величины X.
(Ответ: 
)
10.14. Доказать, что при выполнении условий
и 
для математического ожидания случайной величины справедливо равенство
.
(Указание: Воспользоваться соотношением 
)
10.15. Вероятность обнаружения затонувшего судна за время поиска t задается формулой
.
Определить среднее время поиска, необходимое для обнаружения судна.
(Ответ: 
Указание: Обратить внимание на то, что 
является функцией распределения случайного времени поисков 
, необходимого для обнаружения судна)
10.16. Определить математическое ожидание m(t) массы радиоактивного вещества спустя время t, если в начальный момент масса вещества была 
, а вероятность распада ядра любого атома в единицу времени постоянна и равна р.
(Ответ: 
Указание: Учесть, что вероятность распада любого фиксированного атома за промежуток времени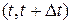 
равна 
и составить дифференциальное уравнение для m(t))
10.17. Определить время полураспада радиоактивного вещества, если вероятность распада ядра любого атома в единицу времени постоянна и равна р. (Время полураспада Тп определяется моментом, когда масса радиоактивного вещества в среднем уменьшается вдвое.)
(Ответ: 
Указание: Воспользоваться решением задачи 10.16)
10.18. Обработка результатов одной переписи показала, что плотность вероятности возраста лиц, занимающихся научной работой, может быть представлена формулой
, 
время в годах, 
.
Определить, во сколько раз число научных работников в возрасте ниже среднего превышает число научных работников в возрасте выше среднего.
(Ответ: 
, то есть научных работников, имеющих возраст меньше среднего (среди научных работников), больше, чем имеющих возраст больше среднего. Средний возраст среди научных работников 
года)
10.19. Найти для распределения Стьюдента, задаваемого плотностью вероятности
,
начальные моменты при 
при 
.
(Ответ: 
при 
, 
Указание: При вычислении интегралов вида 
произвести замену переменных 
, приводящей к бета-функции, а последнюю выразить через гамма-функцию)
10.20. Случайная величина X подчиняется бета-распределению, т. е. имеет плотность вероятности
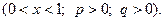
Найти начальный момент k-гo порядка.
(Ответ: 
)
10.21. Найти математическое ожидание и дисперсию случайной величины, имеющей в интервале 
плотность вероятности 
.
(Ответ: 
)
10.22. Выразить центральный момент 
через начальные моменты.
(Ответ: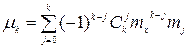 
, где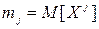 
)
10.23. Выразить начальный момент через центральные моменты и математическое ожидание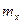 
.
(Ответ: 
, где 
)
Дата добавления: 2014-12-23; просмотров: 676; Мы поможем в написании вашей работы!; Нарушение авторских прав |