Краткая теоретическая часть. Математическое ожидание и дисперсия случайной величины X, имеющей плотность вероятности , вычисляются по формулам

Математическое ожидание 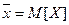и дисперсия случайной величины X, имеющей плотность вероятности , вычисляются по формулам

,

.

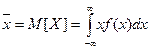Математические ожидания и дисперсии непрерывных случайных величин обладают такими же свойствами, что и аналогичные вероятностные характеристики дискретных случайных величин. Среднее квадратическое отклонение определяется формулой

.

Для симметричного закона распределения характеристикой рассеивания случайной величины может служить срединное отклонение Е, определяемое из условия

.

Начальный момент k-ro порядка m_k и центральный момент k-ro порядка вычисляются по формулам

,

Для существования моментов нечетного порядка необходима абсолютная сходимость соответствующих интегралов.

Тест

1. Выберите те из следующих предложений, которые являются верными. Математическое ожидание и дисперсия непрерывных случайных величин…

а) являются вероятностными характеристиками, не имеющими ничего общего с аналогичными характеристиками дискретных случайных величин

б) обладают такими же свойствами, что и аналогичные вероятностные характеристики дискретных случайных величин

в) как и в случае дискретных случайных величин, определяют положение реализации случайной величины на числовой прямой и рассеянье случайной величины соответственно

2. Математическое ожидание 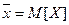и дисперсия непрерывной случайной величины X, имеющей плотность вероятности , вычисляются по формулам

а)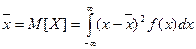

б) ,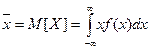

.

в)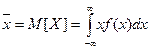

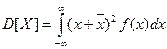
г)

3. Начальный и центральный моменты -го порядка – это числовые характеристики

а) дискретных случайных величин

б) непрерывных случайных величин

в) и дискретных, и непрерывных случайных величин

4. Начальный и центральный моменты -го порядка непрерывной случайной величины определяются формулами:

а)

,

где - математическое ожидание , - возможные значения случайной величины , - соответствующие им вероятности, - математическое ожидание

б)

,

где - математическое ожидание , - возможные значения случайной величины , - соответствующие им вероятности, - математическое ожидание

в)

,

где - математическое ожидание случайной величины , - плотность вероятности случайной величины

г)

,

где - математическое ожидание случайной величины , - плотность вероятности случайной величины