Задачи для самостоятельной работы

9.1. Определить математическое ожидание числа приборов, давших отказ за время испытаний на надежность, если испытанию подвергается один прибор, а вероятность его отказа р.

(Ответ: )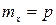

9.2. Считая, что вес тела с одинаковой вероятностью может быть равен любому целому числу граммов от 1 до 10, определить, при какой из трех систем разновесов:

а) 1, 2, 2, 5, 10;

б) 1, 2, 3, 4, 10;

в) 1, 1, 2, 5, 10

среднее число необходимых для взвешивания гирь будет наименьшим, если при взвешивании разрешается гири ставить только на одну чашку, а подбор гирь при взвешивании осуществляется так, чтобы использовать наименьшее возможное число гирь.

(Ответ: а) ; б) ; в) )

9.3. Испытуемый прибор состоит из пяти элементов. Вероятность отказа для элемента с номером равна

Определить математическое ожидание и дисперсию числа отказавших элементов, если отказы элементов независимы.

(Ответ: )

9.4. Производятся независимые испытания трех приборов. Вероятность отказа каждого прибора соответственно равна , и . Доказать, что математическое ожидание числа отказавших приборов равно .

(Указание: Для доказательства достаточно вычислить , где )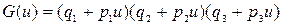

9.5. Определить математическое ожидание числа приборов, отказавших в работе за время испытаний, если вероятность отказа для всех приборов одна и та же и равна р, а число испытуемых приборов п.

(Указание: Составить производящую функцию )

9.6. В лотерее имеется выигрышей стоимостью — стоимостью , ..., т_п — стоимостью . Всего билетов N. Какую стоимость билета следует установить, чтобы математическое ожидание выигрыша на один билет равнялось половине его стоимости?

(Ответ: )

9.7. Первый игрок бросает 3, а второй 2 одинаковых монеты. Выигрывает и получает всё 5 монет тот, у которого выпадает большее число гербов. В случае ничьей игра повторяется до получения определенного результата. Каково математическое ожидание выигрыша для каждого из игроков?

(Ответ: Для первого , для второго - , то есть игра проигрышная для второго игрока)

9.8. Три игрока А, В, С играют на следующих условиях: в каждой партии участвуют двое; проигравший уступает место третьему; первую партию играют А с В. Вероятность выигрыша в каждой партии для каждого игрока равна . Игра продолжается до тех пор, пока один из игроков не выиграет подряд 2 раза. При этом он получает т рублей. Каково математическое ожидание выигрыша для каждого игрока:

а) после первой партии при условии, что А ее выиграл;

б) в начале игры?

(Ответ: а) ; б)

Указание: Ввести в рассмотрение величины - математические ожидание выигрышей игроков соответственно при условии, что игрок А выиграл у В. Для этих величин справедливы равенства , которые составляют систему уравнений для нахождения неизвестных . )

9.9. Три игрока А, В, С играют на следующих условиях: в каждой партии участвуют двое; проигравший уступает место третьему; первую партию играют А с В. Вероятность выигрыша в каждой партии для каждого игрока равна . Игра продолжается до тех пор, пока один из игроков не выиграет подряд 2 раза; при этом он получает сумму выигрыша, равную числу всех сыгранных партий. Каково математическое ожидание выигрыша для игроков А и С до начала игры?

(Ответ: )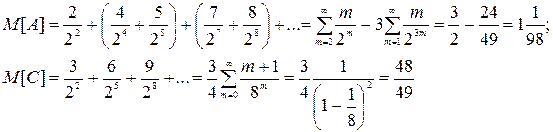

9.10. Автоматическая линия при нормальной настройке может выпускать бракованное изделие с вероятностью р. Переналадка линии производится после первого же бракованного изделия. Найти среднее число всех изделий, изготовленных между двумя переналадками линии.

(Ответ: )

9.11. Вероятность приема позывного сигнала одной радиостанции другой радиостанцией равна 0,2 при каждой посылке. Позывные подаются каждые 5 сек. до тех пор, пока не будет получен ответный сигнал, принимаемый достоверно. Общее время прохождения позывного и ответного сигналов равно 16 сек. Найти среднее число подаваемых позывных сигналов до установления двусторонней связи.

(Ответ: )

9.12. Найти математическое ожидание и дисперсию числа изделий, изготовляемых на поточной линии при нормальной настройке за период между двумя переналадками, если при нормальной настройке вероятность изготовления бракованного изделия равна р, а переналадка производится после изготовления k-ro бракованного изделия.

(Ответ: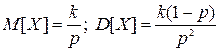

Указание: Ряд суммируется с помощью формулы , где )

9.13. Условная вероятность отказа прибора, вычисленная в предположении о неработоспособности т элементов, имеет вид:

а) для прибора А

б) для прибора В

Найти математическое ожидание числа неработоспособных элементов, приводящих к отказам приборов А и В.

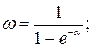(Ответ: а) , где б)

Указание: Суммирование ряда производится по формулам )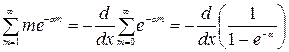

9.14. Блокировочная схема, состоящая из реле А, включенного последовательно с двумя реле В и С, соединенными параллельно, должна обеспечить замыкание цепи между клеммами / и // (рис. 12). Вследствие неисправности реле А может не сработать с вероятностью 0,18, а реле В и С — с одинаковыми вероятностями, равными 0,22. Определить среднее число включений до схемы до первого отказа блокировочной схемы.

(Ответ: 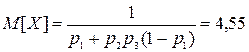, где )

9.15. Прибор имеет элементы А, В и С, уязвимые к космическому излучению и дающие отказ при попадании в них хотя бы одной частицы. Отказ прибора наступает в случае отказа элемента А или совместного отказа элементов В и С. Определить математическое ожидание числа частиц, попадание которых в прибор приводит к его отказу, если условные вероятности попадания в элементы А, В и С частицы, уже попавшей в прибор, соответственно равны 0,1; 0,2; 0,2.

(Ответ: )

9.16. Прибор имеет п элементов типа А и т элементов типа В. В случае отказа элементов типа А они не заменяются, а работа прибора продолжается до тех пор, пока в схеме есть хотя бы один исправный элемент типа А. Отказы элементов типа В устраняются так, что число исправных элементов типа В в схеме остается постоянным. Отказ любого из исправных элементов прибора равновозможен. Определить среднее число отказов элементов, приводящих к полному отказу прибора, т. е. к выходу из строя всех п элементов типа А.

(Ответ: )

9.17. Доказать, что дисперсия числа появлений события при однократном производстве опыта не превосходит 1/4.

(Указание: исследовать на максимум дисперсию как функцию вероятности появления события)

9.18. Определить условия, для которых третий центральный момент биномиального распределения равен нулю.

(Ответ: обращается в 0 при )

9.19. Функция распределения случайной величины X задана равенством

где - наибольшее целое число, меньшее .

Доказать, что если 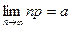, то .

(Указание: Рассмотреть дисперсию как функцию вероятности появления события)

9.20. Из урны, содержащей весьма большое число белых и черных шаров, смешанных в равной пропорции, вынимаются последовательно 10 шаров. Шары, вынутые до первого появления черного шара, возвращаются в урну; первый появившийся черный шар и все последующие перекладываются во вторую, первоначально пустую, урну. Определить математическое ожидание числа белых и черных шаров во второй урне.

Решить ту же задачу в предположении, что число X вынутых шаров является случайным и подчиняется закону Пуассона с параметром а = 10, т. е.

.

(Ответ: В обоих случаях математическое ожидание числа черных шаров во второй урне равно5, а белых – в случае (а) - , в случае (б) - )

9.21. Игра заключается в том, что монету бросают до появления герба. Если герб выпал при k-м бросании монеты, то игрок А получает k рублей от игрока В. Сколько рублей должен уплатить игрок А игроку В перед началом игры для того, чтобы математические ожидания проигрыша для каждого игрока равнялись нулю (чтобы игра была «безобидной»)?

(Ответ: Два рубля)

9.22. Автоколонна может прибыть на станцию обслуживания в любой момент времени. При организации дежурства п ремонтных рабочих способом А среднее число обслуживаемых машин равно пр. При организации дежурства способом В будет обслужено: машин, если автоколонна прибудет в первую половину суток; пр машин, если автоколонна прибудет в третью четверть суток; 0,5пр машин, если автоколонна прибудет в четвертую четверть суток.

При каких значениях р следует предпочесть организацию дежурства способом В?

(Ответ: При )

9.23. Рабочий обслуживает п однотипных станков, расположенных в ряд с равными промежутками а. Закончив обслуживание какого-либо станка, рабочий переходит к тому станку, который раньше других потребовал обслуживания. Предполагая, что неполадка в любом из п станков равновероятна, вычислить среднее значение длины одного перехода рабочего.

(Ответ:

Указание: При отыскании вероятностей того, что случайная длина перехода равна , воспользоваться формулой полных вероятностей, приняв в качестве гипотезы 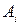то, что рабочий в данный момент стоит у -го станка)

9.24. Случайная величина X может принимать целые положительные значения с вероятностями, убывающими в геометрической прогрессии. Выбрать первый член и знаменатель прогрессии q так, чтобы математическое ожидание величины X было равно 10, и вычислить при этом условии вероятность .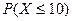

(Ответ: )

9.25. Случайная величина X может иметь любое целое положительное значение п с вероятностью, пропорциональной . Найти математическое ожидание X.

(Ответ: )

9.26. Случайная величина X имеет распределение

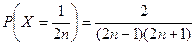( =1, 2, …).

Найти

(Ответ: )

9.27. Игра состоит в том, что повторяются независимые опыты, в каждом из которых событие А может произойти с вероятностью р. Если событие А произошло в 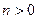опытах подряд, а в ( )-м опыте не произошло, то первый игрок получает от второго игрока у^п рублей. Если же п=0, то первый игрок платит второму игроку 1 рубль. Требуется найти величину у при условии, что игра будет «безобидной», т. е. математическое ожидание выигрыша для обоих игроков равно 0. Рассмотреть пример .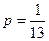

(Ответ: руб.)

9.28. Из сосуда, содержащего, т белых и п черных шаров, извлекаются шары до тех пор, пока не появится белый шар. Найти математическое ожидание числа вынутых черных шаров и его дисперсию, если каждый шар после извлечения возвращался.

(Ответ: )

9.29. Даны два ящика с белыми и черными шарами; в первом ящике при общем числе шаров N находится М белых шаров, а во втором ящике имеется белых шаров при общем числе 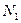шаров. Опыт состоит в том, что из каждого ящика вынимается один шар, который перекладывается в другой ящик, после чего шары перемешиваются. Определить математическое ожидание числа белых шаров в первом ящике по окончании указанных k опытов. Рассмотреть случай .

(Ответ:

Указание: Составить конечноразностное уравнение для математического ожидания числа белых шаров 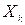, находящихся в первой урне после k опытов: )

9.30. Связь с дрейфующей станцией могут поддерживать п радиостанций. Вступает в двустороннюю связь та, которая первой примет позывные дрейфующей станции, причем это событие равновероятно для всех п радиостанций ( ). Дрейфующая станция будет устанавливать связь т раз. Определить вероятность того, что радиостанция № 1 вступит в двустороннюю связь k раз. Найти для нее же математическое ожидание и дисперсию числа вступлений в двустороннюю связь.

(Ответ: )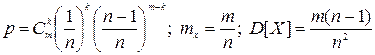

9.31. Независимые испытания аппаратуры повторяются до тех пор, пока не произойдет отказ. Вероятность отказа от испытания к испытанию не меняется и равна р. Найти математическое ожидание и дисперсию числа безотказных испытаний.

(Ответ: , где )

9.32. Двое поочередно бросают монету до тех пор, пока у обоих не выпадает одинаковое число гербов. Вероятность ого, что после бросаний у обоих будет одинаковое, количество гербов, равна

.

Определить математическое ожидание числа бросаний.

(Ответ: , так как ряд расходится при )