
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приложения. Приложение 1. Таблица значений функции 0,0
Приложение 1. Таблица значений функции 
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 | 0,3989 0,3970 0,3910 0,3814 0,3683 0,3521 0,3332 0,3123 0,2897 0,2661 0,2420 0,2179 0,1942 0,1714 0,1497 0,1295 0,1109 0,0940 0,0790 0,0656 0,0540 0,0440 0,0355 0,0283 0,0224 0,0175 0,0136 0,0104 0,0079 0,0060 0,0044 0,0033 0,0024 0,0017 0,0012 0,0009 0,0006 0,0004 0,0003 0,0002 |
Приложение 2. Таблица значений функции 
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 | 0,0000 0,0797 0,1585 0,2358 0,3108 0,3829 0,4515 0,5161 0,5763 0,6319 0,6827 0,7287 0,7699 0,8064 0,8383 0,8664 0,8904 0,9109 0,9281 0,9426 0,9545 0,9643 0,9722 0,9786 0,9836 0,9876 0,9907 0,9931 0,9949 0,9963 0,9973 0,9981 0,9986 0,9990 0,9990 0,9995 0,9997 0,9998 0,9999 0,9999 |
Приложение 3 .Таблица значений вероятности 

| ||||||||
| 0,3173 | 0,6065 | 0,8013 | 0,9098 | 0,9626 | 0,9856 | 0,9948 | 0,9982 |
Приложение 4 (лицевая сторона бланка)
Финансовая академия при Правительстве РФ
Кафедра теории вероятностей и математической статистики
Расчетный бланк
К лабораторной работе
"Обработка результатов наблюдений"

 Вариант№ Группа
Вариант№ Группа

 Выполнил Проверил
Выполнил Проверил
 |


 0 x
0 x
Таблица 1
| № интервалов | ||||||||
Границы интервалов 
| ||||||||
Среднее значение в интервале 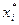
| ||||||||
Число наблюдений в интервале 
| ||||||||
Частота в интервале 
|
Приложение 5 (обратная сторона бланка)
k =  Р0 = с = Р0 = с =
|
 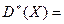 
|
  S = S = 
|
| X2 = r = Pr = |
Выводы:
Ответы к упражнениям
§1 1.7.  ;1.8.
;1.8.  ;1.9.
;1.9. 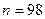 ;1.10.
;1.10.  ;1.11.
;1.11.  ;1.12.
;1.12.  ;1.13.
;1.13.  ;1.14.
;1.14.  ;1.15.
;1.15.  и
и 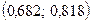 ;1.16.
;1.16.  ;1.18.
;1.18.  ;1.19.
;1.19.  ;1.20.
;1.20.  ;1.21.
;1.21.  ;1.22.
;1.22.  ;1.23.
;1.23.  ;1.24.
;1.24.  ;1.25.
;1.25.  ;1.26.
;1.26.  .
.
§2 2.1. Zн = 5 > 2,58 = Zкр  Н0 отв.;2.2.
Н0 отв.;2.2. = 22,1 < 36,2 =
= 22,1 < 36,2 = 
 Н0 прин. ;2.3. Fн= 3,39 >2,7 = Fкр
Н0 прин. ;2.3. Fн= 3,39 >2,7 = Fкр  Н0 отв.;2.4. Fн= 1,34 < 2,49 = Fкр
Н0 отв.;2.4. Fн= 1,34 < 2,49 = Fкр 
 , Tн =12,06 > 2,06 = Tкр
, Tн =12,06 > 2,06 = Tкр 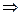 Н0 отв.;2.5. Fн= 1,07 < 4,63 = Fкр
Н0 отв.;2.5. Fн= 1,07 < 4,63 = Fкр 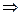
 , Tн =1,46 < 2,53 = Tкр
, Tн =1,46 < 2,53 = Tкр 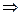 Н0 прин. ;2.6. Fн= 1,48 < 9,12 = Fкр
Н0 прин. ;2.6. Fн= 1,48 < 9,12 = Fкр 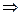
 , |Tн| =0,25 < 1,89 = Tкр
, |Tн| =0,25 < 1,89 = Tкр  Н0 прин.;2.7.
Н0 прин.;2.7.  = 8,63 < 42,6 =
= 8,63 < 42,6 = 
 Н0 прин. ;2.8. Zн = 3,3 > 1,645 = Zкр
Н0 прин. ;2.8. Zн = 3,3 > 1,645 = Zкр  Н0 отв.;2.9.
Н0 отв.;2.9.  = 8,166 < 15,1 =
= 8,166 < 15,1 = 
 Н0 прин. ;2.10.
Н0 прин. ;2.10.  = 2,139 < 11,1 =
= 2,139 < 11,1 = 
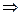 Н0 прин.
Н0 прин.
§4 4.1.0,89;4.2.  ,
, 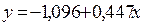 ; 4.3.0,81; 4.4.
; 4.3.0,81; 4.4.  ,
,  ; 4.4.
; 4.4.  ,
,  ; 4.5. 0,82; 4.6.
; 4.5. 0,82; 4.6.  ;4.7.
;4.7.  ;4.8. R = 0,94,
;4.8. R = 0,94,  .
.
§5 5.1.0,688;5.3.  ; 5.4. a)-0,952; б) –1,01; в) 166,852; 5.5.0,83; 5.6.6140; 5.7.0,954; 5.8.661.
; 5.4. a)-0,952; б) –1,01; в) 166,852; 5.5.0,83; 5.6.6140; 5.7.0,954; 5.8.661.
Заключение
Исторически первой появились некоторые области статистики объектов нечисловой природы (в частности, задачи оценивания доли брака и проверки гипотез о ней) и одномерная статистика. Математический аппарат для них проще, поэтому на их примере обычно демонстрируют основные идеи математической статистики.
Лишь те методы обработки данных, т.е. математической статистики, являются доказательными, которые опираются на вероятностные модели соответствующих реальных явлений и процессов. Речь идет о моделях поведения потребителей, возникновения рисков, функционирования технологического оборудования, получения результатов эксперимента, течения заболевания и т.п. Вероятностную модель реального явления следует считать построенной, если рассматриваемые величины и связи между ними выражены в терминах теории вероятностей. Соответствие вероятностной модели реальности, т.е. ее адекватность, обосновывают, в частности, с помощью статистических методов проверки гипотез.
Невероятностные методы обработки данных являются поисковыми, их можно использовать лишь при предварительном анализе данных, так как они не дают возможности оценить точность и надежность выводов, полученных на основании ограниченного статистического материала.
Вероятностные и статистические методы применимы всюду, где удается построить и обосновать вероятностную модель явления или процесса. Их применение обязательно, когда сделанные на основе выборочных данных выводы переносятся на всю совокупность (например, с выборки на всю партию продукции).
В конкретных областях применений используются как вероятностно-статистические методы широкого применения, так и специфические. Например, в разделе производственного менеджмента, посвященного статистическим методам управления качеством продукции, используют прикладную математическую статистику (включая планирование экспериментов). С помощью ее методов проводится статистический анализ точности и стабильности технологических процессов и статистическая оценка качества. К специфическим методам относятся методы статистического приемочного контроля качества продукции, статистического регулирования технологических процессов, оценки и контроля надежности и др.
Широко применяются такие прикладные вероятностно-статистические дисциплины, как теория надежности и теория массового обслуживания. Содержание первой из них ясно из названия, вторая занимается изучением систем типа телефонной станции, на которую в случайные моменты времени поступают вызовы - требования абонентов, набирающих номера на своих телефонных аппаратах. Длительность обслуживания этих требований, т.е. длительность разговоров, также моделируется случайными величинами. Большой вклад в развитие этих дисциплин внесли член-корреспондент АН СССР А.Я. Хинчин (1894-1959), академик АН УССР Б.В.Гнеденко (1912-1995) и другие отечественные ученые.
Дата добавления: 2014-12-23; просмотров: 241; Мы поможем в написании вашей работы!; Нарушение авторских прав |