Сравнение выборочной исправленной дисперсии с заданной дисперсией нормальной генеральной совокупности

Рассмотрим ещё один класс задач, связанный с параметрической проверкой статистических гипотез. в которых применяется критерий .

Рассматривается выборка, предположительно извлечённая из нормально распределённой генеральной совокупности с заданной дисперсией . Однако случайная величина, которой в данном случае является дисперсия, не подчиняется нормальному закону распределения. В этом случае применяется критерий .

На практике нулевая гипотеза Н₀: E(S²) = проверяется, если нужно проверить точность приборов, методики контроля ритмичности работы и т.д. В качестве критерия проверки нулевой гипотезы примем случайную величину

.

Здесь S² - выборочная исправленная дисперсия. Можно показать, что случайная величина К имеет теоретическое распределение с (n - 1)-й степенью свободы.

Итак, по данным эмпирического ряда вычисляется величина

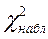
, (2.13)

затем по таблице 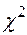определяется критическое значение 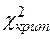. Если > , то нулевую гипотезу отвергают, т.е. принимают одностороннюю альтернативную гипотезу Н₁: S² > . В противном случае можно считать различие исправленной выборочной дисперсии S² и гипотетической дисперсии незначимым.

Пример 2.8.Ритмичность работы кассира сбербанка по приёму коммунальных платежей определяется дисперсией времени обслуживания клиентов, которая не должна превышать величины D = 1 мин². Результаты 30 наблюдений за работой нового кассира приведены в таблице:

Проверим нулевую гипотезу о допустимой ритмичности работы новичка при уровне значимости 0,05.

Решение.Введем новую переменную и составим вспомогательную таблицу:

	ni									Среднее
	xi = ti-7,5	-2	-1
	xi2									1,8

D_в(t) = 1,8 , 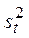= = 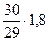1,86.

Вычислим статистику по формуле (2.13) и применим критерий .

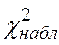= = =53,94.

(0,05; 29) = 42,6, > .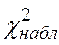

Нулевая гипотеза о равенстве дисперсий должна быть отвергнута, следовательно, новый кассир пока ещё не вошёл в требуемый ритм работы.

Рассмотренные примеры применения основных правил проверки статистических гипотез не исчерпывают всех сфер применения указанной теории, являющейся частью более общей теории планирования эксперимента. Дополним вышеперечисленные правила таблицей, позволяющей легче ориентироваться в многообразных задачах проверки параметрических и непараметрических гипотез (см. Таблица 2.1).

Рассмотрим пример применения этой таблицы.

Пример 2.9. Вероятность приобрести выигрышный билет в некоторой лотерее р= 0,2. Предприятие приобрело 100 лотерейных билетов, из которых в результате очередного розыгрыша лотереи оказалось 14 выигрышных билетов. При уровне значимости 0,05 требуется проверить правильность случайной выборки.

Решение.Проверим нулевую гипотезу Н₀ о равенстве фактической вероятности выигрыша сотрудника предприятия, приобретшего на предприятии один лотерейный билет, гипотетической вероятности. Согласно таблице критериев проверки статистических гипотез выбираем 4-ую строку таблицы. Критерий проверки имеет вид:

.

Вычислим наблюдаемое значение критерия

= -1,5.

По условию задачи критическая область – двусторонняя. Найдём правую критическую точку из равенства = 0,5 – 0,025 == 0,475, отсюда z_крит = 1,96. Таким образом < z_крит. Следовательно, нет оснований отвергнуть нулевую гипотезу. Наблюдаемая относительная частота 0,14 незначимо отличается от гипотети ческой вероятности 0,2.

№ п/п	задача	статистика	Теоретическое. распределение
1.	Сравнение выборочной средней с математическим ожиданием нормальной ГС		N(0;1) H0 принимается, если
2.	Сравнение двух выборочных средних из нормальных ГС с равными n и		- ,, -
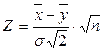
3.	Сравнение выборочных средних (две выборки) из нормальных ГС с разными, но заданными и		- ,, -
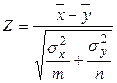
	Сравнение доли признака в выборке с вероятностью p		- ,, -
5.	Сравнение выборочных средних (две выборки) с большими и независимыми выборками любого распределения		Приближенный N(0;1) H0 принимается, если
6.	Сравнение выборочной исправленной дисперсии с заданной норм. ГС		«хи-квадрат»
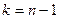
7.	Сравнение выборочного распределения долей признаков с теоретическим распределением		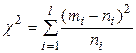«хи-квадрат»
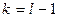
8.	Сравнение выборочной гистограммы с плотностью нормального закона		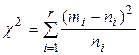«хи-квадрат»
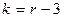
9.	Сравнение средних (две малые независимые выборки из нормальных ГС) с неизвестными, но равными дисперсиями		Распределение Стьюдента
10.	Сравнение двух дисперсий нормальных ГС	(sx > sy)	Распределение Фишера- Снедекора