Проверка гипотезы о равенстве математических ожиданий при равных неизвестных дисперсиях

Пусть теперь для тех же выборок обе генеральные дисперсии неизвестны, но одинаковы, т.е. .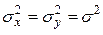

Рассмотрим их выборочные средние и исправленные дисперсии:

, , , .

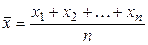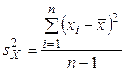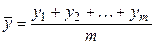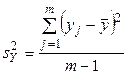Известно, что , - нормально распределенные случайные величины. Величины 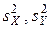подчинены ²-распределению соответственно с ( n- 1) и (m - 1) степенями свободы. Поскольку случайные величины X и Y независимы, то величина

U =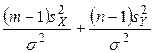

имеет ²-распределение с (m+n-2) степенями свободы, а величина распределена нормально: .

Поэтому нормализованная случайная величина

V = (2.5)

имеет стандартное нормальное распределение N(0, 1), а отношение

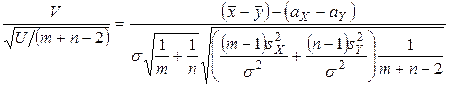
имеет распределение Стьюдента с (m+n-2) степенями свободы. Таким образом, если гипотеза H₀: a_х = a_у верна, то величина

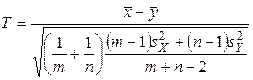(2.6)

имеет распределение Стьюдента с (m+n-2) степенями свободы. Эта величина используется в качестве критерия для проверки гипотезы H₀.

В качестве альтернативной к данной гипотезе рассмотрим гипотезу H₁: 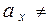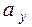.Зададим уровень значимости a и построим двустороннюю критическую область. Левое критическое значение определим из уравнения

F_n+m-2(x₁) = 0,5 ,

где F_n+m-2(x) - функция распределения Стьюдента с (n+m-2) степенями свободы, а правое критическое значение по свойству чётности соответствующей функции плотности: x₂=-x₁. Далее проверка гипотезы аналогична изложенному в предыдущем разделе.

Пример 2.4. Для того чтобы проверить технологию изготовления нового кваса "Будь здоров", периодически отбирают случайным образом 10 бутылок и находят концентрацию сахара. В следующей таблице приведены данные по стандартной партии (Х) и по очередной проверяемой (Y).

Выдвигаем нулевую гипотезу H₀: a_х = a_у при конкурирующей гипотезе H₁: a_х ≠ a_у. Положим уровень значимости α= 0,1. Проверим H₀

Решение.Введём новые переменные u = x – 9,43; v = y- 9,24. Составим служебные таблицы для новых переменных:

№
U	2,5			-0,5	0,5		-2	-0,5	-1	0,5	0,5
U2	6,5			0,25	0,25			0,25		0,25	13,5

№
V		0,5	1,5	-1			-0,5		0,5
V2		0,25	2,25				0,25		0,25		9,5

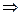
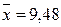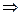
Вычисление средних значений и стандартных отклонений дают следующие результаты ; 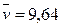, , 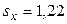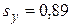. Учитывая, что в данном примере n = m = 10, мы можем вычислить критерий T_набл.:

= 0,335.

По данному значению α и по числу степеней свободы (n+m-2) = 18 находим по таблице критическое значение Т_кр2 == 1,73. Следовательно, область принятия имеет вид (-1,73; 1,73).

Поскольку найденное значение T_набл. попадает в область принятия, то гипотезу H₀ принимается. В этой задаче мы в первом приближении предполагали, что дисперсии обеих выборок статистически не различимы. Ниже будет показано, как оценить существенно ли отличаются дисперсии двух выборок из нормально распределённой совокупности.