Проверка гипотезы о равенстве математических ожиданий при известных дисперсиях

Пусть (x₁, x₂,…, x_n) - выборка объема n значений случайной величины X, подчиненной нормальному закону распределения с параметрам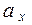и и , причем значение параметра 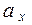неизвестно, а значение дисперсии известно. Аналогично пусть (y₁, y₂,…, y_m) - выборка объема m значений случайной величины Y, также имеющей нормальный закон распределения с неизвестным параметром 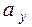и известную дисперсию .

Будем считать, что случайные величины X и Y независимы. В этих предположениях проверим нулевую гипотезу H₀: 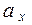= 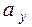Построим критерий проверки этой гипотезы. Рассмотрим последовательно величины:

и .

Величина имеет нормальное распределение с параметрами и , аналогично величина - нормальное распределение с параметрами и 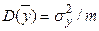, поэтому величина ( ) распределена по нормальному закону с параметрами 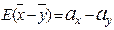=0. Для независимых случайных величин Х и Y получим . Определим статистику

(2.3)

Утверждение: Если гипотеза H₀ верна, то случайная величина Z имеет стандартное нормальное распределение.

В качестве альтернативной гипотезы H₁ выберем, например, такую: 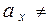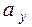.Для заданного уровня значимости α критические значения находим из условий

P(Z < z₁) = 0,5 α и P(Z > z₂) = 0,5 α .

Отсюда видно, что z₁ = –z₂, а правое критическое значение z₂ получим из уравнения

.

В частности, если m =n, = = , то получим формулу (2.2). Кроме того, если сравнивается только один вариационный ряд с известным нормальным законом , то формула (2.3) принимает вид (2.1).

Замечание. Данный критерий применяют, например, когда производится обследование характеристик товаров, выпускаемых на аналогичных предприятиях. Предстоит выяснить, носит ли различие среднего выпуска статистический характер (различие незначимо) или обусловлено организацией производства (различие значимо).

Пример 2.3. Количество продаж дезодоранта «Афродита» по месяцам (в тыс. флаконов), производимого на фабриках "Московские зори" (МЗ) и «Вестерн» (В), заданы в следующих таблицах:

Проверим гипотезу H₀ о равенстве математических ожиданий при альтернативной гипотезе, что они не равны. Предполагается, что у этих фабрик стандартные отклонения известны и равны соответственно =3 и =2. Положим уровень значимости =0,1.

Решение.Для удобства вычислений введем новые случайные величин U=X-110, V=Y-110.. Составим служебные таблицы для новых переменных:

№
U	5,5	0,3	2,7	-2,3	-1,2	1,9	5,8	0,7	13,4

№
V	0,8	1,1	3,6	2,5	2,4	3.7	-1,5	12,6

Вычислим средние значения, получим

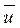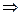
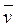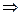
= 1,675 = 111,675; =1,8 = 111,8.

.

Из уравнения

Ф(z₂) = 0,5 - = 0,5 - 0,05 = 0,45

находим правое критическое значение z₂ = 1,65.

Поскольку Z_набл Î (-1,65; 1,65), то гипотеза H₀ принимается.