Сравнение выборочной средней с математическим ожиданием нормальной генеральной совокупности при известной дисперсии

Пусть (x₁, x₂,…, x_n) – выборка объёма n извлечена из некоторой генеральной совокупности, распределённой по нормальному закону с известным математическим ожиданием a и дисперсией 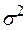. Необходимо сравнить выборочную среднюю с генеральной средней.

Нулевая гипотеза H₀: E(X) = a.

Построим критерий проверки этой гипотезы. Рассмотрим величину .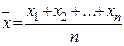

Её математическое ожидание E ( 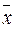) = a, дисперсия D( ) = ,

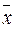следовательно ( )= .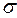

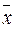Введем статистику

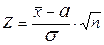. (2.1)

Утверждение: Если гипотеза H₀ верна, то случайная величина Z имеет стандартное нормальное распределение.

Пример 2.1. Рост абитуриентов среди поступающих юношей-подростков в Финансовую Академию при Правительстве РФ распределён по нормальному закону с математическим ожиданием a = 181 см и среднеквадратическим отклонением s = 3 см. Для выдачи медицинских справок об основных физиологических показателях были случайно отобраны 8 абитуриентов, полученные данные о их росте приведены в следующей таблице:

Проверим гипотезу о равенстве средней по выборке и математического ожидания по этому показателю у обследованных абитуриентов. Положим уровень значимости a= 0,1;

Решение. Введем переменную U = X – 180. Составим вспомогательную таблицу:

№
U	5,5	0,3	2,7	-2,3	-1,2	1,9	-5,8	0,7	0,7	2,5

Вычислим среднее значение по выборке . Получим 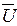= 2,5 , следовательно 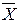= 182,5 см. Применяя формулу (2.1), вычислим

Z_набл = = 1,5

Из уравнения 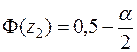=0,5 – 0,05 = 0,45 находим по таблице функции Лапласа (приложение 2) правое критическое значение z₂ = 1,65. Поскольку , то нулевая гипотеза H₀ принимается.