
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения
1.1.Привести числовой пример и описание простой случайной выборки (повторной и бесповторной).
1.2.Привести числовой пример и описание механической выборки.
1.3.Привести числовой пример и описание типической выборки.
1.4. Привести числовой пример и описание серийной выборки.
1.5. Привести пример двухступенчатой выборки.
1.6. Имеются 4 стержня следующих размеров: 20 см (2 стержня), 21 см и 22 см. производится повторная выборка двух стержней. Составить все возможные выборочные распределения для  и
и  . Найти
. Найти  ,
,  и проверить их связь с соответствующими генеральными характеристиками.
и проверить их связь с соответствующими генеральными характеристиками.
1.7. В выборке объемом 500 единиц, произведенной для определения процента всхожести зерна, установлена частота доброкачественных зерен 0,96. Определить, с какой степенью надежности может быть принят процент всхожести, равный 96 %, если допустимая погрешность при его определении равна  2 %.
2 %.
1.8.Для определения процента изделий 1-го сорта в партии (доли признака) производится случайная повторная выборка объемом в 100 единиц. В выборке установлено, что число изделий первого сорта 75 единиц. Определить доверительные границы для процента изделий первого сорта во всей партии, которые могут быть гарантированы с доверительной вероятностью 0,99.
1.9. Определить необходимый объем выборки, который гарантировал бы ошибку выборки, не превышающую 0,1 с вероятностью 0,999. Ориентировочно известно, что  . Выборка случайная повторная.
. Выборка случайная повторная.
1.10.В условиях предыдущей задачи определить необходимый объем выборки, если значение  неизвестно.
неизвестно.
1.11. Для определения доли брака продукции отобрано 1000 единиц, из которых бракованных оказалось 50. Выборка случайная повторная. Найти с вероятностью 0,954 пределы возможного отклонения выборочно установленной частоты брака от доли брака во всей совокупности.
1.12. Сколько семян надо отобрать для определения процента всхожести, чтобы с вероятностью 0,977 можно было утверждать, что отклонение частоты доброкачественных семян от их доли, равной 0,99, не превышало по абсолютной величине 0,02?
1.13. Численность повторной выборки – 800 единиц. Доля признака 0,4. Найти с вероятностью 0,8, в каких пределах находится отклонение частоты от доли признака.
1.14. Проверено 3000 электрических лампочек. Доля брака в этой партии составляет 0,15. Какова вероятность того, что отклонение выборочно установленной частоты брака от доли брака во всей продукции не превышает по абсолютной величине 0,01 (выборка повторная).
1.15. Для определения доли изделий первого сорта в партии из 1000 штук была произведена выборка объемом в 100 единиц. В отобранной пробе частота изделий первого сорта оказалось равной 0,75. Оценить с вероятностью 0,90 доверительные границы для определяемой доли. Расчет произвести для повторной и бесповторной выборки.
1.16.Определить необходимый объем выборки, который ту же предельную погрешность, что и в предыдущей задаче, обеспечит с вероятностью 0,99.
1.17. Построить график зависимостей необходимого объема выборки п от определяемой доли признака р, предельной погрешности  и доверительной вероятности Р0. При построении задаться значениями остальных параметров произвольно.
и доверительной вероятности Р0. При построении задаться значениями остальных параметров произвольно.
1.18. Из партии готовой продукции объемом в 10000 единиц для определения доли брака производится бесповторная выборка. Определить необходимый объем этой выборки, который с вероятностью 0,99 гарантировал бы ошибку, не превышающую 0,1. Определить с вероятностью 0,96, в каких границах заключено отклонение выборочной средней от генеральной средней.
1.19. Для определения средней урожайности массива пшеницы площадью в 400 га был произведен случайный отбор 50 опытных участков, каждый площадью 0,25 га. Выборочная средняя урожайность оказалась равной 19 ц/га, а среднее квадратическое отклонение 1,5 ц/га. Найти с вероятностью 0,99 возможные пределы для определяемой средней урожайности.
1.20. Какой объем выборки необходимо взять, чтобы с вероятностью 0,98 можно было бы гарантировать отклонение выборочной средней от генеральной средней не более чем на 1 %? Предварительная выборка дала 
1.21. Обследуется средняя продолжительность телефонного разговора. Сколько телефонных разговоров должно быть зафиксировано, чтобы с вероятностью 0,997 можно было бы утверждать, что отклонение выборочной средней от генеральной средней не превосходит 10 секунд, если среднее квадратическое отклонение равно 2,5 минуты?
1.22.Производится выборочное обследование возраста читателей массовых библиотек. Имеется 30000 читательских карточек. Сколько карточек необходимо взять для обследования, чтобы с вероятностью 0,99 можно было бы утверждать, что выборочная средняя отклонится от генеральной средней не более чем на 1 год? Среднее квадратическое отклонение принять равным 5 годам.
1.23.Испытание крепости отобранных 150 нитей дали следующие результаты:
| Крепости нити (в г) | 210 – 250 | 250 – 290 | 290 – 330 | 330 – 370 |
| Число нитей |
Определить с вероятностью 0,99 среднюю крепость нитей всей партии.
1.24. При проверке бухгалтерской отчетности универмага установлено, что 80 счетов, случайно отобранных из 6000, имеют среднее дебетовое сальдо  руб. при среднем квадратическом отклонении
руб. при среднем квадратическом отклонении  руб. Найти с вероятностью 0,9 возможные пределы для среднего сальдо всех 6000 счетов.
руб. Найти с вероятностью 0,9 возможные пределы для среднего сальдо всех 6000 счетов.
1.25.В отрасли, включающей 1500 заводов, была составлена случайная выборка из 60 заводов. Результаты выборочного обследования показали, что на заводе работает в среднем 328 человек при среднем квадратическом отклонении 25 человек. С какой вероятностью можно утверждать, что отклонение выборочно установленного среднего числа работающих  на одном заводе от среднего числа работающих на одном заводе во всей отрасли не превосходит 5 человек.
на одном заводе от среднего числа работающих на одном заводе во всей отрасли не превосходит 5 человек.
1.26.Пусть X1, X2,…, X9 – выборка из равномерного распределения на отрезке [6; 16]. F*(x) – соответствующая выборочная функция распределения. Найдите вероятность 
1.27.Пусть X1, X2, X3, X4, X5 – выборка из равномерного распределения на отрезке [10; 18], F*(x) – соответствующая
выборочная функция распределения. Найдите  .
.
1.27. Случайная величина X (время работы элемента) имеет показа тельное распределение с плотностью 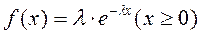 .
.
По эмпирическому распределению среднего времени работы элемента в час методом моментов найдите точечную оценку неизвестного параметра l
| xi | 2,5 | 7,5 | 12,5 | 17,5 |
| mi |
1.29.Случайная величина X распределена по закону Пуассона  .
.
Дана выборка случайной величины X в следующей таблице:
| xi | ||||
| mi |
(mi – число опытов, в которых событие наблюдалось xi раз). Найти точечную оценку неизвестного параметра 
1.30.По выборке x1 = 5; x2 = 4; x3= 2; x4= 4; x5= 3; x6= 2 найти точечную оценку параметра р геометрического распределения:  где Х – случайная величина, означающая число испытаний до первого появления события А, а р – вероятность появления события А в одном испытании.
где Х – случайная величина, означающая число испытаний до первого появления события А, а р – вероятность появления события А в одном испытании.
1.31.Даны результаты 8 независимых измерений одной и той же величины прибором, не имеющим систематических ошибок: 369, 376, 318, 422, 388, 401, 372, 383 м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина не известна.
1.32.Даны результаты 8 независимых измерений одной и той же величины прибором, не имеющим систематических ошибок: 365, 379, 315,425, 386,403, 374, 381 м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина известна и равна 373 м.
1.33. Совместное частотное распределение признаков задано таблицей:
| Y X | x = 1 | x = 2 |
| y = 2 | ||
| y = 3 | 0 | 3 |
Найдите эмпирический коэффициент корреляции
1.34. Значение признаков X и Y заданы на множестве  таблицей частот:
таблицей частот:
| X Y | x = 200 | x = 400 | x = 100 |
| y = 2 | |||
| y = 3 |
Из  без воз вращения извлекаются 30 элементов.
без воз вращения извлекаются 30 элементов.  и
и  – средние значения в выборочной совокупности. Найдите
– средние значения в выборочной совокупности. Найдите  .
.
1.35. Три игральные кости, красная, зелёная и синяя подбрасываются до тех пор, пока не выпадет 20 различных с учётом цвета комбинаций очков. Пусть Si число очков на красной и зелёной костях в i-й комбинации,  – среднее арифметическое значение всех этих чисел, i = 1, 2,…, 20. Найдите математическое ожидание и дисперсию среднего значения
– среднее арифметическое значение всех этих чисел, i = 1, 2,…, 20. Найдите математическое ожидание и дисперсию среднего значения 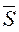 .
.
1.36.Признак X(к) задан на множестве  следующей таблицей:
следующей таблицей:
| k | |||||||||||||||
| X(k) |
Из  извлекается случайная повторная выборка объёма 10. Найдите математическое ожидание дисперсию среднего значения
извлекается случайная повторная выборка объёма 10. Найдите математическое ожидание дисперсию среднего значения 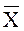 признака X в выборке.
признака X в выборке.
1.37.В некотором городе сделали прививку от гриппа 38% всех жителей, не сделали – 12%, но не заболели. Известно, что объём бесповторной выборки составляет 15% от числа всех жителей города. Пусть  –выборочная доля, сделавших прививку, nв – число отобранных жителей, не сделавших прививку и не заболевших. Найдите приближённо
–выборочная доля, сделавших прививку, nв – число отобранных жителей, не сделавших прививку и не заболевших. Найдите приближённо  (примем, что человек не заболел после того, как сделал прививку).
(примем, что человек не заболел после того, как сделал прививку).
1.40.Значения признака в генеральной совокупности заданы таблицей частот:
| Интервал | 11 – 15 | 15 – 19 | 19 – 23 | 23 – 27 |
| Частота |
Из этой совокупности производится бесповторная выборка объёма 6. Найдите среднеквадратическую ошибку в приближённом равенстве  .
.
1.41.Статистические данные о результатах ЕГЭ в трёх школах приведены в таблице:
| № п/п | Число школьников | Средний бал | Среднее квадратическое отклонение |
ЕГЭ сдавали на нейтральной территории в разных аудиториях. Условия экзамена во всех аудиториях одинаковы. В одной из них оказалось 35 человек. Найти математическое ожидание и дисперсию среднего бала по результатам, полученным в данной аудитории.
Дата добавления: 2014-12-23; просмотров: 538; Мы поможем в написании вашей работы!; Нарушение авторских прав |