
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка генеральной дисперсии
Пусть


Поскольку заменяются две величины (  и
и  ), то это вызывает смещение оценки
), то это вызывает смещение оценки 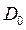 :
:
 . (1.22)
. (1.22)
Покажем это .
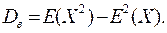
Известно что

.
Пусть Х1, Х2,…, Хi ,...,Xn - независимые случайные величины, каждая из которых имеет один и тот же закон распределения с числовыми характеристиками:  и D(Xi)=D0. Пусть
и D(Xi)=D0. Пусть 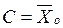 подставим в (*), тогда:
подставим в (*), тогда: 
Найдем E[Dв]: 





Итак  Что и требовалось доказать.
Что и требовалось доказать.
При больших п смещение невелико, им можно пренебречь, но при малых выборках оно существенно.
Таким образм,  есть несмещенная оценка дисперсии или
есть несмещенная оценка дисперсии или
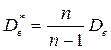 . (1.23)
. (1.23)
Тогда исправленное среднее квадратическое отклонение имеет вид:
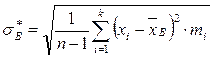 . (1.24)
. (1.24)
Для интервальной оценки используется выражение 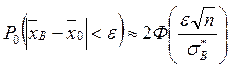 , где
, где 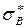 находится по формуле (1.24).
находится по формуле (1.24).
Замечание. Однако для больших выборок можно считать, что  . В случае малых выборок (п < 30) пользуются исправленной дисперсией по формуле (1.24).
. В случае малых выборок (п < 30) пользуются исправленной дисперсией по формуле (1.24).
По закону больших чисел  является состоятельной оценкой для
является состоятельной оценкой для  генеральной дисперсии. А так как множитель
генеральной дисперсии. А так как множитель  при
при  , то
, то  также является состоятельной оценкой для
также является состоятельной оценкой для 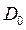 . Оценка
. Оценка  , строго говоря, не является эффективной оценкой для
, строго говоря, не является эффективной оценкой для  , однако при наличии нормального распределения ее можно считать приближенно эффективной.
, однако при наличии нормального распределения ее можно считать приближенно эффективной.
Замечание. Если известно точное значение математического ожидания «  » для n измерений, то E(Xi) =
» для n измерений, то E(Xi) =  где хi – отдельные измерения. Исправленная (несмещённая) дисперсия находится по формуле
где хi – отдельные измерения. Исправленная (несмещённая) дисперсия находится по формуле
 (1.25)
(1.25)
Действительно.
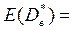


 , т.е. E(D*в) = D0 .
, т.е. E(D*в) = D0 .
Пример 1.19. В ящике содержатся стержни трех размеров (N = 3): 12 см, 14 см и 16 см с соответствующими долями 0,1; 0,3; 0,6. Производится повторная выборка двух стержней (n = 2). Найти все возможные выборочные распределения и построить законы распределения для 
 и
и  . Проверить на данном примере справедливость равенств
. Проверить на данном примере справедливость равенств  .
.
Решение.Определим количество возможных выборок:
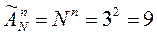 .
.
Закон распределения генеральной совокупности представлен в следующей в таблице
| X | |||
| P | 0,1 | 0,3 | 0,6 |
Вычислим генеральные характеристики :
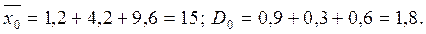
Все выборочные законы представлены в следующей таблице.
| № выборки | |||||||||

| |||||||||

| 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | 1 1 | |||

| |||||||||

| |||||||||

| 0,01 | 0,03 | 0,06 | 0,03 | 0,09 | 0,18 | 0,06 | 0,18 | 0,36 |
Проверим, что  .
.
По данным последней таблицы получим строим законы распределения для  и Dв и находим соответствующие характеристики.
и Dв и находим соответствующие характеристики.

| 
| |||||
| P | 0,01 | 0,06 | 0,21 | 0,36 | 0,36 |
 ,
, 
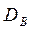
| 
| |||

| 0,46 | 0,42 | 0,12 |
E[Dв]=0,42+0,48=0.9/
Итак, 

 ,
,
Откуда следует:  и
и 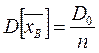 при n = 2.
при n = 2.
Пример 1.20. Даны результаты 6 независимых измерений одной и той же величины прибором, не имеющим систематических ошибок: 36; 37; 32; 43; 39; 41. Найдите несмещенную оценку дисперсии ошибок измерений, если истинная длина неизвестна.
Решение. Представим исходные данные в виде таблицы:
| xi | ||||||
| р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Вычислим последовательно
 ;
;




Отсюда 

Пример 1.21. В условиях предыдущей задачи найдите несмещённую оценку дисперсии ошибок измерений, если истинная величина известна и равна 37,8.
Решение В этом случае в формулу подставляется не выборочное среднее, а истинная величина:
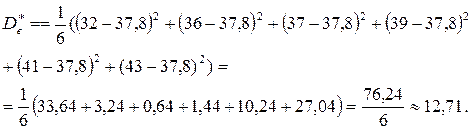
Дата добавления: 2014-12-23; просмотров: 511; Мы поможем в написании вашей работы!; Нарушение авторских прав |