
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Генеральной средней
Точечная оценка генеральной средней.
Пусть  ,
,  .
.
Выборка рассматривается как п повторных независимых испытаний. Результат каждого испытания есть случайная величина xi, закон распределения которой совпадает с генеральным распределением, т.е.  и
и 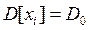 . После n испытаний, получены n попарно независимых одинаково распределенных случайных величин,.
. После n испытаний, получены n попарно независимых одинаково распределенных случайных величин,.
 - случайная величина.
- случайная величина.
Всего выборок можно произвести  . Определив вероятность каждой выборки и составив закон распределения для
. Определив вероятность каждой выборки и составив закон распределения для  , найдем
, найдем
 ,
,
отсюда  и
и  - несмещенная оценка
- несмещенная оценка  .
.
 - состоятельная оценка
- состоятельная оценка  (по теореме Чебышева.
(по теореме Чебышева.
Рассмотрим дисперсию
 (1.17)
(1.17)
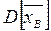 при
при  будет иметь минимально возможное значение, следовательно
будет иметь минимально возможное значение, следовательно  - эффективная оценка
- эффективная оценка  .
.
Итак, точечная оценка генеральной средней удовлетворяет всем необходимым требованиям.
Интервальная оценка генеральной средней.
 (1.18)
(1.18)
Формула (1.18) получена на основании частного случая теоремы Ляпунова, т.е. теоремы Лапласа для одинаково распределенных случайных величин при больших объемах выборки. Но 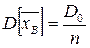 согласно (1.17), следовательно,
согласно (1.17), следовательно,
 . (1.19)
. (1.19)
Тогда
 . (1.20)
. (1.20)
ЗамечаниеЕсли значение  неизвестно, то егоследует заменить "хорошей" точечной оценкой. Считая, что.
неизвестно, то егоследует заменить "хорошей" точечной оценкой. Считая, что. 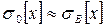 получим аналог формулы (1.20):
получим аналог формулы (1.20):
 . (1.21)
. (1.21)
Пример 1..13.Определяется средний рабочий стаж  большой группы рабочих. Произведена случайная повторная выборка 900 личных листков. Средний рабочий стаж в выборке оказался равным 15,5 годам, а среднее квадратическое отклонение 4,8 года. С какой вероятностью можно утверждать, что отклонение выборочной средней от генеральной не превысит 0,5 года.
большой группы рабочих. Произведена случайная повторная выборка 900 личных листков. Средний рабочий стаж в выборке оказался равным 15,5 годам, а среднее квадратическое отклонение 4,8 года. С какой вероятностью можно утверждать, что отклонение выборочной средней от генеральной не превысит 0,5 года.
Решение.По условию  . Найти
. Найти  .
.
Вычисляем  . По таблице находим
. По таблице находим  , сле-довательно, по формуле (1.20) доверительная вероятность
, сле-довательно, по формуле (1.20) доверительная вероятность  .
.
Пример 1.14. По данным предыдущего примера найти доверительные границы при оценке генеральной средней, которые можно гарантировать с вероятностью 0,9500.
Решение. По условию 
 Найти
Найти  и
и  .
.
Так как по формуле (1.20 )  где
где  по таблицам находим t = 1,96.
по таблицам находим t = 1,96. 
Доверительные границы будут:
 или
или 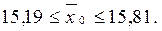
Пример 1.15.В условиях предыдущего примера определить необходимый объем выборки, при котором ошибка не превысит 0,5 с доверительной вероятностью 0,9990.
Решение. По условию Po = 0,9990; 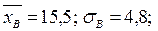
 Найти п.
Найти п.
По таблицам  определяем
определяем  Из равенства
Из равенства  находим
находим 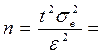
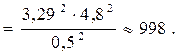
Пример 1.16. Случайная величина Х имеет показательное распределение (например, время бесперебойной работы устройства) с плотностью

В таблице дан эмпирический закон распределения времени работы этого устройства
| Время работы | 0 - 20 | 20 - 40 | 40 - 60 | 60 - 80 |
| Число устройств |
Методом моментов найти точечную оценку параметра l
Дата добавления: 2014-12-23; просмотров: 310; Мы поможем в написании вашей работы!; Нарушение авторских прав |