КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эмпирическая ковариация
Пусть 
и 
заданы на совокупности 
.
Cov(X,Y) – ковариация признаков X, Y в генеральной совокупности объема N. Тогда ковариация выборочных средних определяется следующими соотношениями:
- в случае повторной выборки, (1.31)
- в случае бесповторной выборки. (1.32)
Совместное частотное распределение признаков имеет вид
| X Y | x1 | x2 | …… | xk |
| y1 | m11 | m12 | …… | m1k |
| y1 | m21 | m22 | …… | m2k |
| : : : | : : : | : : : | …… | : : : |
| yl | ml1 | m l2 | …… | m lk |
где mij – частота пары (xi ,yj).
Эмпирическая ковариация на основе такой таблицы определяется по формуле
. (1.33)
Эмпирический коэффициент корреляции признаков определяется: 
. (1.34)
Пример 1.24. Совместное частотное распределение признаков
задано таблицей :
| X Y | x1 = 2 | x2 =3 |
| y1 =2 | ||
| y2 =3 |
Найти эмпирический коэффициент корреляции
Решение. 
Находим отдельные частотные распределения признаков
, 
.
.
;
.
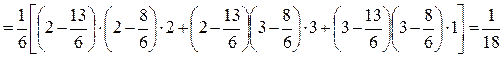Пример 1.25. Три интегральные кости разных цветов подбрасываются до тех пор, пока не выпадет 18 различных с учетом цвета комбинаций очков.
Пусть Si – сумма очков на всех 3-х костях в i-ой комбинации, 
среднее арифметическое всех этих сумм, i = 1, 2,…,18. Найдите математическое ожидание и дисперсию среднего значения 
Решение.xi – число очков на каждой из костей соответственно x1,x2 и x3 – независимы, одинаково распределены и заданы таблицей:
| xi | ||||||
| р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Комбинации различные, следовательно выборка – бесповторная,
объем её n=18, N=63= 216.
; 
;
;
;
.
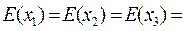
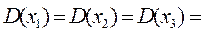
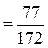Пример 1.26. Признак Х(к) задан на множестве 
таблицей:
| K | ||||||||||||
| Х(к) |
Из 
извлекается случайная повторная выборка объема 7. Найдите математическое ожидание и дисперсию среднего значения 
признака Х в выборке.
Решение. Генеральная совокупность имеет закон распределения:
| Х(к) | |||
| р | 4/12 | 3/12 | 5/12 |
Ее объем N = 12, объем повторной выборки n = 7 Последоваьельно вычисляем:
.
Пример 1.27. В некотором городе болельщики футбольной команды А составляют 24%, команды В 30%. Известно, что объём бесповторной выборки составляет 14% от числа жителей города. Пусть 
– выборочная доля болельщиков команды А, 
– число отобранных болельщиков команды В. Найдите Cov ( 
, ) (приближенно).
Решение.Пусть 
Пусть 
Х и Y – несовместные случайные величины. Их законы распределения, а также совместный закон рапсределения представлены в таблицах;
| Х | ||
| Р | 0,76 | 0,24 |
| Y | XY | ||||
| Р | 0,7 | 0,3 | Р |
E(Х) = 0.24; E(Y)= 0,3; E(ХY) = 0;
D(Х)= 0,24 - 0,0576 = 0,1824; D(Y) = 0,3 - 0,009 = 0,21;
n = 0,14N;
cov(Х,Y )= E(ХY) - E(Х) E(Y) = 00,24 0,3 = - 0,072.
.
Отсюда в нашем примере
0,06192.
Пример 1.28. Значения признака Х в генеральной совокупности заданы таблицей частот
| Интервал | 10 - 14 | 14 - 18 | 18 - 22 |
| Частота |
Из этой генеральной совокупности производится бесповторная выборка объёма 5. Найдите среднеквадратическую ошибку в приближённом равенстве 
Решение.Представим исходные данные в виде такой таблицы
| |||
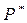
| 5/25 | 9/25 | 11/25 |
Далее по формуле (1.29)
.
Отсюда 
.
Дата добавления: 2014-12-23; просмотров: 289; Мы поможем в написании вашей работы!; Нарушение авторских прав |