Межгрупповая дисперсия

Пусть совокупность объёма n разбита на к групп, n_i – число элементов i-й группы. Пусть Х – некоторый признак, он встречается в каждой их групп, при этом –групповое среднее в i-ой группе.. Тогда среднее во всей совокупности можно высислит по формуле:

(1.35)

Это озачает, что среднее значение признака во всей совокупности есть взвешенное среднее групповых средних.

Аналогично можно вычислить – i-ую групповую дисперсию. Взвешенное среднее групповых дисперсий называют среднейя групповой дисперсией:

(1.36)

Кроме того, вычисляют межгруппоую дисперсию:

. (1.37)

Общая дисперсия равна сумме средней групповой и межгрупповой дисперсии:

, (1.38)

где первое слагаемое характеризует разброс групповых средних 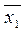, ,… , а второе слагаемое характеризует среднюю изменчивость в каждой группе.

Пример 1.29.

Статистические данные о результатах экзамена в 5-ти группах приведены в таблице:

№№ Групп	Число студентов ni	Средний балл	Среднее квадратичное отклонение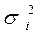
ФК2-13
ФК2-14
ФК2-15
ФК2-16
ФК2-17

Экзамен проводился в разных аудиториях, условия экзамена во всех аудиториях были одинаковы.. В одной из них оказалось 30 человек. Найти математическое ожидание и дисперсию среднего балла по результатам, полученным в данной аудитории.

Решение.N = 24 + 22 + 22 + 21 + 23 = 112; n = 30.

1) Вычислим средний бал:

2) Межгрупповая дисперсия:

3) Средняя групповая дисперсия:

4) Общая дисперсия: