О смысле ошибок первого и второго рода

Как видно из определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы H₀ и H₁, то ошибки первого рода превратятся в ошибки второго рода и наоборот. Тем не менее, в большинстве практических ситуаций путаницы не происходит, поскольку принято считать, что нулевая гипотеза H₀ соответствует состоянию «по умолчанию» (естественному, наиболее ожидаемому положению вещей) — например, что обследуемый человек здоров, или что проходящий через рамку металлодетектора пассажир не имеет запрещённых металлических предметов. Соответственно, альтернативная гипотеза H₁ обозначает противоположную ситуацию, которая обычно трактуется как менее вероятная, неординарная, требующая какой-либо реакции.

С учётом этого ошибку первого рода часто называют ложной тревогой — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня.

Соответственно, ошибку второго рода иногда называют пропуском события — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).

Определение. Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают α (отсюда название α-errors). Вероятность ошибки второго рода обозначается β (отсюда β-errors). Величина (1 − β)— мощность критерия.

Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода.

В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением и является уровень значимости. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности - к увеличению риска ошибки второго рода (пропуск запрещённого предмета).

Итак, выбирается критерий, т.е. статистика t(x₁ ,… .x_n) и критическая область. затем задают уровень значимости критерия α. При этом область значений критерия разбивают на части: область принятия гипотезы H₀ и область отклонения (критическая область К). Вероятность отклонения гипотезы H₀ в точности совпадает с уровнем значимости: P( t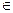K) = . Для двусторонней гипотезы вся ситуация отражена на рисунке 2.1.

Рисунок 2.1

Критическую область в этом случае можно задать в виде двух неравенств

K= {t < К₁} {t > K₂},

критические значения К₁ и К₂ находим по заданному уровню значимости α из уравнений

P(t < К₁) = α /2 и P(t > K₂) = α /2.

Дальнейшее изложение требует знания некоторых стандартных статистических распределений. Напомним их определения.

Пусть Z₁, Z₂,…,Z_k распеределены по стандартному нормальному закону N(0,1).

Случайная величина Y= Z₁² +Z₂² +…+Z_k² распределена по закону, который называется распределением c² с k степенями своботы и обозначается c²(k).

Распределение случайной величины , где X и Y независимы и X~N(0,1), и Y~c²(k), называется распределением Стьюдента с с k степенями своботы и обозначается t(k).

Распределение отношения где X и Y независимы и X~c²(k), и Y~c²(l), называется распределением Фишера с k и l степенями своботы и обозначается F(k,l).

Для каждого из этих определений методами теории вероятностей можно найти функцию плотности f(x), а также функцию распределения F(x). Однако практически этими распределениями пользуются с помощью таблиц, в которых приведены критические значения критериев для различной доверительной вероятности и определенном числе стпеней свободы.