Сравнение генеральных средних по выборкам одинакового объема при равных известных дисперсиях.

Пусть (x₁, x₂,…, x_n) и (y₁, y₂,…, y_n) – выборки одного и того же объёма n из нормальных распределений и соответственно, причем значение известно.

Далее будем считать, что случайные величины X и Y независимы. В этих предположениях проверим нулевую гипотезу H₀: 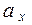= 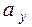. Построим критерий проверки Z этой гипотезы. Рассмотрим величину Z:

. (2.2)

Если гипотеза верна, вновь полученная случайная величина Z имеет стандартное нормальное распределение N(0,1).

Пример 2.2. Количество продаж молока по неделям (в тыс. литров), реализуемого в супермаркетах "Просто продукты" (ПП) и «Крестовский» (К), заданы в следующих таблицах:

Проверим гипотезу H₀ о равенстве математических ожиданий при альтернативной гипотезе, что они не равны. Предполагается, что для этих супермаркетов стандартные отклонения продаж молока известны и равны = 2. Зададим уровень значимости = 0,1.

Решение. Применив смещение обеих случайных величин на х⁰ = 10, т.е. введя переменные U=X-10, V=Y-10, составим служебные таблицы для новых переменных:

№
U	5,5	0,3	2,7	-2,3	-1,2	1,9	-5,8	-5,8	0,7	-4

№
V	0,8	1,1	3,6	2,5	3.7	3.7	2,4	3.7	-1,5	20,0

Последовательно получим:

,

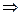
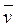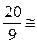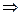
= 2,222 12,222.

Вычислим статистику Z, применив формулу (2.2):

,

.

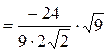Из уравнения Ф(z₂) = 0,5 - = 0,5 - 0,05 = 0,45 по таблице значений функции Лапласа (таблица приложения 2) находим левое критическое значение z₁ = -1,65. Поскольку , то гипотеза H₀ отвергается. Таким образом отличие средних продаж молока в этих супермаркетах значимо.