Сравнение дисперсий двух нормальных распределений

Пусть случайные величины X и Y распределены по нормальному закону. По выборкам значений X объема n и Y объема m требуется проверить нулевую гипотезу H₀ о равенстве дисперсий этих случайных величин: ²(X) = ²(Y).

Как обычно предположим вначале, что математические ожидания X и Y известны и рассмотрим случайную величину

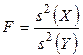, s_x > s_y. (2.7)

Указанная случайная величина распределена по закону Фишера-Снедекора со степенями свободы (n-1) и (m-1).

Пример 2.5.По двум независимым выборкам значений нормально распределенных случайных величин X и Y, объемы которых равны 9 и 6, найдены выборочные дисперсии = 23,27 и = 8,91. При уровне значимости = 0,1 проверить двустороннюю нулевую гипотезу H₀: D(X) = D(Y) .

Решение.Поскольку s_X > s_Y ,то находим значение критерия Фишера-Снедекора: . Число степеней свободы 8 и 5, а значение , по таблице критических значений распределения Фишера-Снедекора находим F_кр = 4,82. Поскольку F_набл < F_кр, нулевая гипотеза принимается.