
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Распределение долей признаков
Критерий 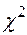 используют еще в одном простом, но очень распространенном случае.
используют еще в одном простом, но очень распространенном случае.
Пусть выполняются следующие условия:
Генеральную совокупность можно разбить на непересекающиеся классы A1, A2, …, доли которых в генеральной совокупности составляют p1, p2, … .
Имеется выборка объема n, пусть выполняются условия:
np1 ³ 5, np2 ³ 5, … . (2.11)
Обозначим далее mi - число представителей выборки, попадающих в категорию i,ni - ожидаемое число в каждом классе, вычисленное согласно нулевой гипотезе. Тогда отклонение выборочных значений от ожидаемых вычисляется по формуле
 , (2.12)
, (2.12)
где суммирование производится по всем классам.
При ранее сформулированных условиях эта статистика подчиняется распределению  с k = (r-1) степенями свободы, где r - число категорий.
с k = (r-1) степенями свободы, где r - число категорий.
Пример 2.7.Данные о различных заболеваниях, определенные на основе сводных данных за год по всем поликлиникам Москвы, представлены в следующей таблице:
| Виды забол. | Грипп | Сердечно-сосудистые | Кишечные | Онкологические | Травматологические | Иммунные |
| Доля | 34% | 18% | 12% | 10% | 15% | 11% |
В некоторой районной поликлинике Москвы аналогичные данные о частоте заболеваний за тот же период представлены ниже.
| Виды забол. | Грипп | Сердечно-сосудистые | Кишечные | Онкологические | Травматологические | Иммунные | |
| mi | |||||||
| ni |
Следует поверить, соответствует ли распределение заболеваний в данной поликлинике общей структуре заболеваний?
Решение.Вычислим общее количество заболеваний за год:
n = 1116 + 502 + 341 + 313 + 415 + 413 = 3100.
Найдем предполагаемые значения теоретических частот по каждой категории и внесём их 3-ю строку таблицы. Пусть уровень значимости = 0,01. Для проверки нулевой гипотезы вычислим критерий  .
.
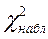 =
= 
 .
.
Поскольку  =15,1 и
=15,1 и 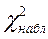 >
>  , то наша гипотеза не принимается. Более подробный анализ слагаемых, из которых состоит сумма наблюдаемых значений критерия, показывает, что основной вклад даёт последнее слагаемое. Районным властям следует обратить внимание на неблагополучную экологическую обстановку, приводящую к росту иммунных заболеваний.
, то наша гипотеза не принимается. Более подробный анализ слагаемых, из которых состоит сумма наблюдаемых значений критерия, показывает, что основной вклад даёт последнее слагаемое. Районным властям следует обратить внимание на неблагополучную экологическую обстановку, приводящую к росту иммунных заболеваний.
Дата добавления: 2014-12-23; просмотров: 248; Мы поможем в написании вашей работы!; Нарушение авторских прав |