Постановка задачи. Пусть задана последовательность значений случайной величины (признака) Х, полученных в результате проведения в одних и тех же условиях п взаимно независимых

Пусть задана последовательность 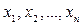значений случайной величины (признака) Х, полученных в результате проведения в одних и тех же условиях п взаимно независимых опытов.

Значения случайной величины Х называются выборкой объема п из генеральной совокупности объема N.

Задача обработки результатов наблюдений случайной величины состоит в следующем:

Построение вариационного ряда или ряда распределения и гистограммы для него.

Определение выборочных оценок числовых характеристик случайной величины.

Определение точности выборкиъ

Определение теоретической функции распределения. Выравнивание статистического ряда.

Проверка согласованности теоретического и статистического распределений, используя критерий .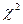

Работа должна быть выполнена на бланке (приложения 4, 5), используя калькулятор и заполнив указанные ниже таблицы.

Результаты достаточно получить с точностью до двух десятичных знаков после запятой. Работу выполнять в следующей последовательности:

1.Построить вариационный (статистический) ряд с длиной интервала и числом интервалов k, указанными в задании.

Отыскав среди значений признака 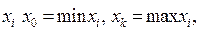находим 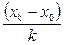. Если 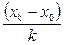соответствует заданному , то 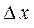и начинаем разбиение на интервалы, а если нет, то уменьшив 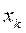или увеличив , добиваемся того, чтобы , при этом "вылетевшие" из промежутка 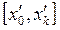значения будем учитывать в соответствующем крайнем интервале. Определим количество значений , приходящихся на каждый i-ый интервал, занося в таблицу Iа "точки" для значений внутри интервала и "зарубки" для значений, находящихся в точности на границе интервала, как показано на примере.

После выполненных подсчетов и проверки заполнить таблицу 3.I (основную).

Таблица 3.I

№ интервала			…		…	К
Границы интервала			...		…
Середина интервала			…		...
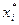
Число наблюдений в интервале			…		…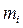
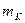
Частота в интервале			…		...

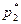
В таблице 3.1 - границы i-го интервала, -середина i-го интервала, - частота в i-ом интервале.

2. Построить для полученного вариационного ряда гистограмму (см. рис. 3.1).

3. Определить выборочное среднее, дисперсию, коэффициент асимметрии и коэффициент эксцесса, используя упрощенные формулы для "ручного" счета.

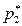
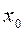
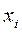
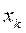
Рисунок 3.1

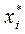Обозначим: , где - среднее значение признака в i-ом интервале; с - среднее значение признака в интервале с наибольшей частотой, принятое в качестве "нуля"; - ширина интервала.

занести результаты в таблицу 3.2

с = …; = … . Таблица 3.2

Интервал

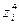
А

В

Д

Е

..

…

…

…

…

…

…

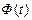
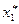
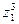
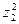
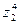
i

..

…

…

…

…

…

…

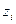
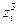
k

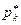
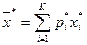
Выборочная средняя:

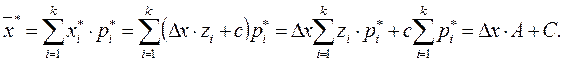
Аналогично выводятся остальные расчетные формулы.

Выборочная дисперсия:

Среднее квадратическое отклонение:

Выборочные центральные моменты 3-го и 4-го порядков:

Коэффициент асимметрии:

Коэффициент эксцесса:

4. Определить точность выборки.

При достаточно большом числе испытаний п можно считать закон распределения нормальным и для оценки точности полученного значения выборочной средней 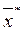применить формулу:

где - среднее значение признака в генеральной совокупности;

- точность (ошибка) выборки;

- доверительная вероятность, т.е. вероятность того, что при данном п отклонение 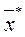от не превзойдет ;

- функция Лапласа (см. Приложение 2).

При заданном значении функции Лапласа по таблицам (приложение 2) найдем аргумент t, а затем из равенства определим точность выборки 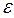при доверительной вероятности . Попробуйте по полученным результатам сделать вывод о качестве выборки.

5.Определить теоретическую функцию распределения, ее параметры. Произвести выравнивание статистического ряда.

Пусть выравнивание проводится с помощью нормального закона распределения. Согласно методу моментов параметры выбираются с таким расчетом, чтобы моменты теоретического распределения были равны соответствующим статистическим моментам.

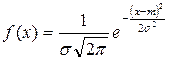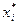Если , то параметры m и выбираем равными соответственно и . , где Значения находим в приложении 3. Строим на рис. 3.1 (где уже построена гистограмма) график по точкам , где - среднее значение признака в интервале.

6. Проверка согласованности теоретического и статистичского распределений.

Согласованность теоретического и статистического распределений проверяется с помощью критерия 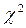(Приложение 3).

,

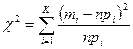где

- см. в приложении 2.

Для статистического ряда (табл. 3.1) определим меру расхождения 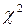по этой формуле (табл. 3.3).

Вычислив , найдем число "степеней свободы" распределения , где k- число интервалов, а S - число связей, накладываемых на частоты . При гипотезе о нормальном распределении число связей равно 3:

Таблица 3.3

Ин-тер-вал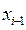

.

.

.

.

.

.

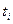
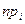
К

Итого :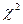

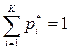(это условие должно выполняться всегда)

.

Число степеней свободы .

Для получения значений и 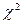по таблицам (приложение 3) найдем вероятность . Если эта вероятность мала, то гипотеза, состоявшая в том, что данная случайная величина имеет закон распределения , отвергается, как мало правдоподобная. Если же эта вероятность значительна, то гипотеза не отвергается или принимается. (Уровень значимости принять 5%). Сделайте необходимые выводы.

Замечание.При использовании приложения 3 иногда приходится пользоваться формулой линейной интерполяции.

;

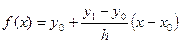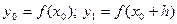
Пример:Пусть При

При

.

Сведите все полученные данные в расчетный бланк, который начертите по образцу, данному в приложениях 4 и 5 (лицевая сторона - приложение 4, обратная сторона - приложение 5).