Случайная повторная выборка для определения оценки доли признака

1) Точечная оценка доли признака.

Пусть . Точечной оценкой этой характеристики будет .

Очевидно, что эта оценка несмещенная.

По теореме Бернулли по вероятности стремится к p - следовательно, оценка состоятельна.

Так как при , следовательно, это эффективная оценка.

2) Интервальная оценка доли признака.

Для неизвестного параметра определяется соответствующий доверительный интервал при заданной вероятности.

Случайная величина при распределена по закону, близкому к нормальному, следовательно,

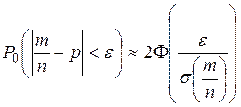, (1.12)

Поскольку 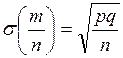,то

. (1.13)

Если р неизвестно, то в силу того, что является точечной оценкой для р, удовлетворяющей всем требованиям, на практике можно заменить .

(1.14)

и 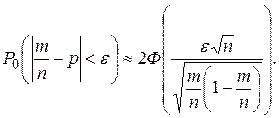(1.15)

Замечание.Можно получить интервальную оценку доли признака р: исходя из следующего. Обозначим , тогда по заданной доверительной вероятности находим по таблицам t (приложение 2), откуда и

Возведем обе части неравенства в квадрат:

В результате преобразований получим квадратное неравенство оносительно р:

Если левая часть имеет корни р₁ и р₂, то в силу того, что коэффициент , , что и является интервальной оценкой р.

Пример 1.9. В случайной повторной выборке объемом 400 единиц, произведенной для определения доли стандартных деталей в партии, частота стандартных деталей оказалась равной 0,950. Определить, с какой доверительной вероятностью процент стандартных деталей в партии может быть принят равным 95 %, если допустимая погрешность при его определении равна ± 2 %.

Решение.По условию п = 400, , Определить Р₀. По формуле (1.15) находим:

Пример 1.10.Для определения процента изделий первого сорта в партии производится случайная повторная выборка объемом 200 единиц. В выборке число изделий первого сорта оказалось равным 160. Определить доверительные границы для процента изделий первого сорта в партии, которые можно принять с доверительной вероятностью равной 0,95.

Решение. По условию

Найти e и доверительные границы ;

Вычисляем

Определим t по известному значению Р₀ (по таблице):

Вычисляем следовательно

,

Отсюда доверительные границы : 0,8-0,055=0,745; и =0,8+0,055=0,855.или 74,5 % и 85,5 % .

Рассмотрим задачу об определнии объема выборки, гарантирующего заданную ошибку. Пусть значение выборочной частоты неизвестно, а доля признака р известна. Найдем объем выборки , который обеспечивает точность выборки с доверительной вероятностью

Т.к. , по таблицам находим

, откуда

Пусть теперь неизвестна доля признака. В этом случае найдем гарантированный минимально необходимый объем выборки , который обеспечивает точность выборки с доверительной вероятностью .

Обозначим . Функция имеет максимум в точке х = 0,5, следовательно, 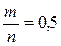и отсюда

. (1.16)

Пример 1.11. Определить необходимый объем выбоки, который дает ошибку выборки, не превышающую 0,05 с доверительной вероятностью 0,991, если известно, что доля признака равна 0,8.

Решение. По условию . Найти n.

1) ПоP₀ = 0,991определяем .

2) По формуле (1.15) определяем

.

Пример 1.12. Определить необходимый объем выборки, который дает ошибку выборки при определении доли изделий первого сорта, не превышающую 0,05 с доверительной вероятностью 0,991, если значение этой доли неизвестно.

Решение. По условию По таблицам .

По формуле (1.16) находим

.

Как видим, объем выборки значительно вырос при неизвестной выборочной частоте.