Выборочные оценки и ошибки выборки

На практике для изучения закономерностейслучайных явлений массового характера. ипользуются именно выборками Выборочный методматематической статистики основывается на законе больших чисел , согласно которому результаты обработки выборки ограниченного объема можно распространять на всю генеральную совокупность. С вероятностной точки зрения важно подчеркнуть, что результат каждого наблюдения в предполагаемом испытании следует рассматривать как случайную величину, поскольку до проведения испытания заранее неизвестно, какое значение примет тот или иной результат наблюдения.

Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) Е(Х) и среднее квадратическое отклонение s. Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной.

Пусть имеется закон распределения генеральной совокупности (на практике обычно неизвестен):

x_i - значение признака, M_i - число объектов с признаком x_i.

Оценки генеральной совокупности (генеральные оценки):

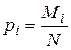_I (1.1)

- доля i-ого признака в генеральной совокупности,

Отметим, что

, т.к. .

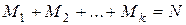(1.2)

- генеральная средняя

(1.3)

- генеральная дисперсия

Функция распределения случайной величины Х:

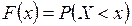(1.4)

Оценки выборочной совокупности (выборочные оценки):

x_i - значение признака,

m_i - число объектов в выборке с признаком x_i;

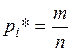(1.5)

- выборочная частота, 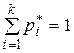, т.к. .

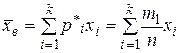(1.6)

- выборочная средняя

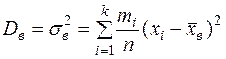(1.7)

- выборочная дисперсия

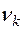
- (1.8)

Выборочный начальный момент k-го порядка

- (1.9)

выборочный центральный момент k-го порядка .

Если обозначить через m_x число наблюдений, при которых значение признака Х меньше х, то частота события « Х < х» равна 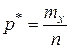, т.е. частота является функцией от х.

Эта функция находится опытным путем, ее называют эмпирической функцией распределения и обозначают:

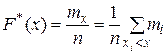(1.10)

Функция при фиксированном хявляется случайной величиной, распределённой по закону:

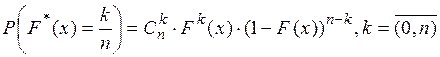(1.11)

т.е. функция 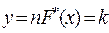распределена по биномиальному закону.

Обозначим любую из генеральных характеристик 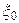, а соответствующую выборочную — .

Определение 3. 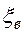называется точечной характеристикой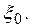

Определение 4. называется ошибкой выборки или точностью выборки.

Ошибки выборки могут быть систематическими (например, если в выборке существует какая-либо правильная повторяемость; такие ошибки могут быть исключены) и случайными (их исключить невозможно, поэтому 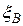и 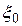совпадать не будут).

Нельзя утверждать, что 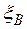удовлетворяет неравенству 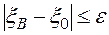, можно лишь указать, с какой вероятностью оно выполняется.

Определение 5. 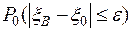называется доверительной вероятностью или надежностью выборки.

Из неравенства 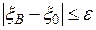следует что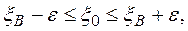

Интервал 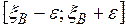называется доверительным интервалом.

Всвою очередь, и 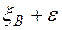называются доверительными границами генеральной характеристики.

Пример 1.5.Пусть генеральная совокупность содержит 300 единиц и имеет следующий закон распределения некоторого количественного признака:

X
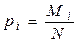
	0,05	0,15	0,40	0,26	0,14

Произведена случайная повторная выборка объемом 30 единиц. Результаты выборочных наблюдений приведены в таблице

X
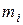
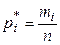
	0,1	0,3		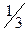0,2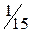

Вычислить генеральную и выборочную средние, генеральную и выборочную дисперсии, а также составить теоретическую и эмпирическую функции распределения.

Решение.. По формуле (1.2) вычислим генеральную среднюю

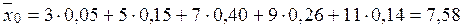
По формуле (1.3) находим генеральную дисперсию:

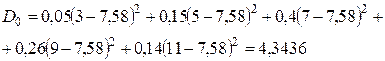
Функция распределения 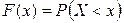имеет вид:

Соответствующие характеристики в выборочной совокупности находим по формулам (1.6) и (1.7):

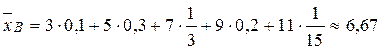
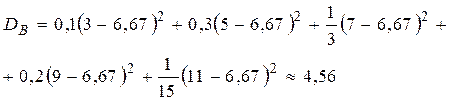
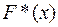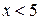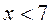Построим эмпирическую функцию распределения по данным выборки. Поскольку наименьшее выборочное значение признака равно 3, то . Значение наблюдалось 3 раза, следовательно, . Значение наблюдалось 12 раз из 30, потому ; значение наблюдалось 3+9+10=22 раза, следовательно,

. При , .

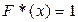Таким образом

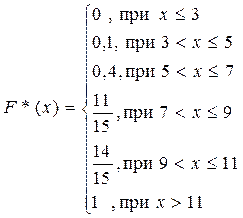
Пример 1.6. В партии из 6000 деталей 120 бракованных. Из этой партии произведена случайная повторная выборка объемом 200 единиц. Среди отобранных деталей оказалось 6 бракованных. Найти генеральную и выборочную доли бракованных деталей.

Решение. По условию доля бракованных деталей в генеральной совокупности равна 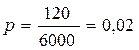(или 2%). Доля или частота бракованных деталей в выборке равна 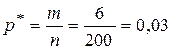(или 3%).

Пример 1.7.Пусть X_1, X_2,…_, X₆ выборка из равномерного распределения на отрезке [7, 17]. 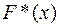соответствующая данной выборке эмпирическая функция распределения. Найти вероятность .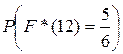

Решение. В каждом испытании вероятность того, что) выбранные числа будут не более 12 равна 0,5, поскольку число 12 – середина отрезка [7, 17], а все возможные числа распределены на указанном отрезке равномерно. Таким образом, запись 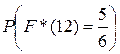означает распределение вероятностей в схеме Бернулли, в которой n = 6, k = 5, p = q = 0,5 , таким образом

.

Пример 1.8.Пусть X_1, X_2,X_3, X₄ выборка из равномерного распределения на отрезке [9, 15]. соответствующая данной выборке эмпирическая функция распределения. Найти вероятность .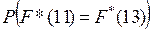

Решение. n = 4, P .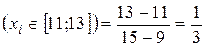

Тогда

= = .

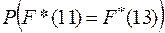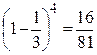Дата добавления: 2014-12-23; просмотров: 28; Нарушение авторских прав