
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Частотные характеристики. Подадим на вход линейного устойчивого звена гармонический сигнал
Подадим на вход линейного устойчивого звена гармонический сигнал
 .
.
После окончания переходного процесса на входе получим установившийся гармонический сигнал той же частоты, но другой амплитуды и сдвинутый по фазе на угол  по сравнению с входным
по сравнению с входным
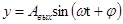 .
.

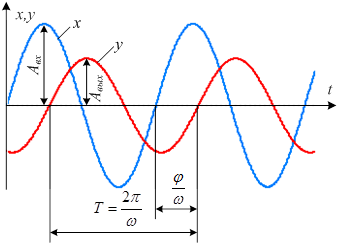
Если изменять частоту входного сигнала, оставляя амплитуду постоянной, то будет изменяться амплитуда выходного сигнала и сдвиг по фазе.
Зависимость отношения амплитуды выходного сигнала к амплитуде входного от частоты называется амплитудно-частотной характеристикой АЧХ
 .
.
Зависимость сдвига фаз между выходными и входными колебаниями называется фазо-частотной характеристикой ФЧХ
 .
.
Примеры графиков АЧХ и ФЧХ приведены ниже
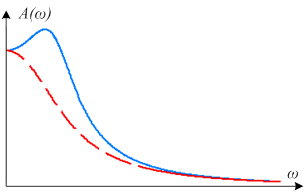

АЧХ с ростом частоты убывает, фазовый сдвиг для большинства реальных звеньев отрицателен (отставание по фазе).
Значение A(ω) характеризует усиление по амплитуде гармонического сигнала частоты ω.
Важную роль играет амплитудно-фазовая характеристика (АФХ) определяемая формулой
 (*)
(*)
Формально W(jω) – комплексный вектор, длина (модуль) которого равен A(ω), а угол в вещественной осью φ(ω). Формула (*) является показательной формой записи комплексного числа. При изменении частоты ω в пределах 0≤ω≤∞ конец вектора описывает кривую, которая собственно и называется амплитудно-фазовой характеристикой АФХ,


Формулу (*) можно записать в другом виде
 ,
,
где  ,
,  - вещественная и мнимая частотные характеристики – проекции вектора W(jω) на оси координат.
- вещественная и мнимая частотные характеристики – проекции вектора W(jω) на оси координат.
Формулы связи:
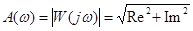
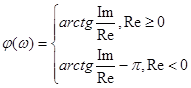


Дата добавления: 2014-12-30; просмотров: 357; Мы поможем в написании вашей работы!; Нарушение авторских прав |