Статические звенья.

1. Усилительное звено

Это безынерционное звено, описываемое уравнением

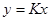
К – коэффициент усиления.

Передаточная функция

.

Простейшим примером может служить делитель напряжения или рычаг

Построим переходную характеристику звена

2. Звено чистого или транспортного запаздывания

Звено описывается уравнением

,

где τ – запаздывание.

Выходной сигнал повторяет входной со сдвигом во времени (запаздыванием) на время τ.

Преобразуя по Лапласу уравнение, в соответствии с теоремой запаздывания получаем

.

Передаточная функции звена

.

Переходная характеристика:

Примером может служить транспортер

, где .

Другой пример – прокатка стали

Толщина может быть измерена только на определенном расстоянии от валов, что приводит к запаздыванию измерения.

С еще одним примером запаздывания сталкивались, наверное, все – регулирование температуры.

3. Апериодическое звено 1 порядка (инерционное)

Звено описывается уравнением:

.

Передаточная функция звена

.

Найдем переходную характеристику звена

.

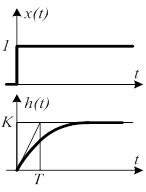
Переходный процесс завершается за время равное (3-4)T. Чем больше время T, тем дольше длится переходный процесс.

Примером являются емкости

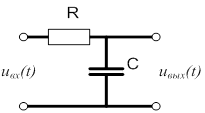
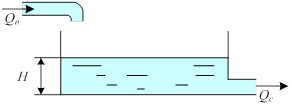
4. Статические звенья 2-ого порядка

Статические звенья 2-ого порядка описываются уравнением

.

Передаточная функция

,

где T₁, T₂ – постоянные времени, положительные числа.

Характеристический полином

.

Звено называется апериодическим, если корни характеристического уравнения действительны и отрицательны.

Корни будут действительны, если дискриминант уравнения неотрицателен, то есть если

, .

В этом случае D(s) разлагается на два сомножителя с действительным корнями

; , .

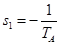Передаточная функция может быть представлена в виде последовательного соединения двух апериодических звеньев 1-ого порядка

.

Примером может служить последовательное соединение двух емкостей.

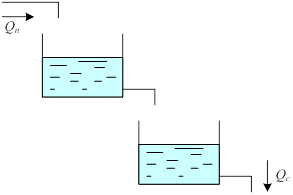
Переходную характеристику можно найти по ее изображению H(s)

.

Разложив H(s) на сумму трех дробей и перейдя к оригиналу

.

График переходного процесса изображен на рисунке, пунктиром показан процесс в инерционном звене.

Звено называется колебательным, если корни характеристического уравнения комплексно-сопряженные. Это происходит при выполнении условия .

Другой формой записи передаточной функции является

,

где ξ – коэффициент демпфирования, для колебательного звена ,

T – постоянная времени; , .

Переходная характеристика получается аналогично предыдущему звену, только комплексно-сопряженные корни дают гармоническую составляющую переходного процесса

,

где , .

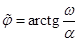График переходной характеристики

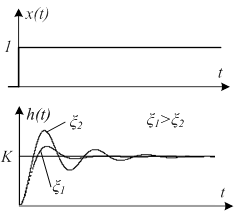
Чем меньше ξ, тем система более колебательная.

Примеры

колебательный контур

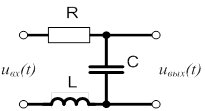
демпфер

При ξ=0 в системе возникают незатухающие колебания, такое звено называется консервативным звеном.

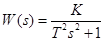
Примером такого звена служит математический маятник.

График переходного процесса

Особенностью устойчивых статических звеньев является то, что переходная характеристика с течением времени стремится к K=W(0), то есть .